Question

If points (1, 0), (0, 1) and (x, 8) are collinear, then the value of x is
(a) 5
(b) -6
(c) 6
(d) -7

Answer 1

Hint: To solve this question we will use the fact that three points are said to be collinear if the area of triangle formed using these three points is zero. Area of triangle, \[\Delta =\dfrac{1}{2}\left| \begin{matrix}
   1 & 1 & 1 \\
   {{x}_{1}} & {{x}_{2}} & {{x}_{3}} \\
   {{y}_{1}} & {{y}_{2}} & {{y}_{3}} \\
\end{matrix} \right|\]. This way we can easily determine the value of x. To get started, first assume the given points from the question as \[\left( {{x}_{1}},{{y}_{1}} \right)=\left( 1,0 \right)\], \[\left( {{x}_{2}},{{y}_{2}} \right)=\left( 0,1 \right)\], \[\left( {{x}_{3}},{{y}_{3}} \right)=\left( x,8 \right)\] . Now, substitute these properly in the determinant and equate it to 0 to find the value of x.

Complete step-by-step solution:
Given that point (1, 0), (0, 1) and (x, 8) are collinear.
We know the fact that when three points are collinear, it means they lie on the same line. Such a set of points cannot form a triangle where all three points must lie on different lines. So, the area of the triangle formed using these three points will be zero.
Area of triangle, \[\Delta =\dfrac{1}{2}\left| \begin{matrix}
   1 & 1 & 1 \\
   {{x}_{1}} & {{x}_{2}} & {{x}_{3}} \\
   {{y}_{1}} & {{y}_{2}} & {{y}_{3}} \\
\end{matrix} \right|\], where, \[\left( {{x}_{1}},{{y}_{1}} \right)=\left( 1,0 \right)\], \[\left( {{x}_{2}},{{y}_{2}} \right)=\left( 0,1 \right)\], \[\left( {{x}_{3}},{{y}_{3}} \right)=\left( x,8 \right)\].
Given that points are collinear \[\Rightarrow \Delta =0\].
Substituting the value in \[\Delta \] we get;
\[\Rightarrow \Delta =\dfrac{1}{2}\left| \begin{matrix}
   1 & 1 & 1 \\
   1 & 0 & x \\
   0 & 1 & 8 \\
\end{matrix} \right|=0\]
Opening the determinant along first column we get;
\[\begin{align}
  & \Rightarrow \dfrac{1}{2}\left| \begin{matrix}
   1 & 1 & 1 \\
   1 & 0 & x \\
   0 & 1 & 8 \\
\end{matrix} \right|=0 \\
 & \Rightarrow \dfrac{1}{2}\left[ 1\left( -x \right)-1\left( 8-0 \right)+1\left( 1-0 \right) \right]=0 \\
 & \Rightarrow \dfrac{1}{2}\left( -x-7 \right)=0 \\
 & \Rightarrow -x=7 \\
 & \Rightarrow x=-7 \\
\end{align}\]
Hence the value of x for which the points (1, 0), (0, 1), and (x, 8) are collinear is -7, which is an option (d).
We can also plot the points and understand that they are collinear as shown below,

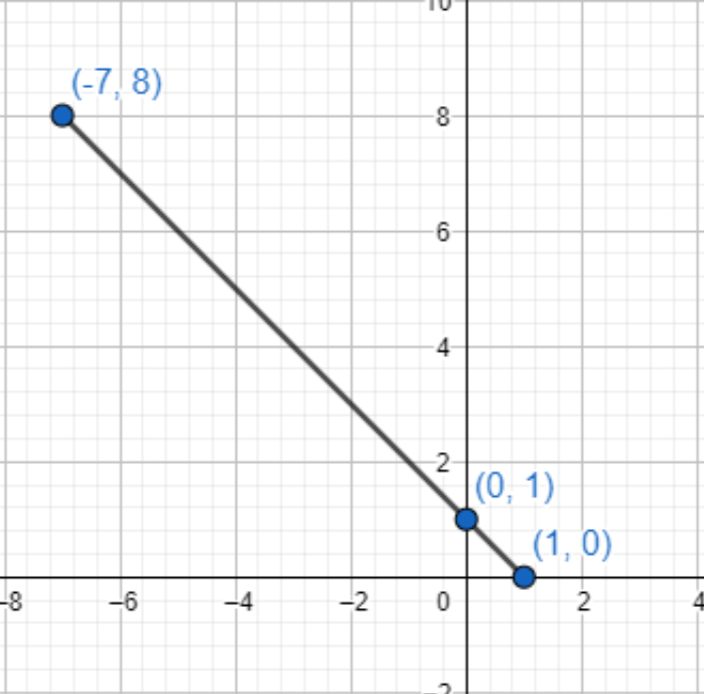
Note: Another way to solve this question is opening the determinant directly without using the area of triangle in determinant form.
We can directly use, \[\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]\] = 0, and substitute value of \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] and \[\left( {{x}_{3}},{{y}_{3}} \right)\] directly to get the answer. The answer anyway would be the same.