Question

If P(2, -1), Q(3, 4), R(-2, 3) and S(-3, -2) be four points in a plane, show that PQRS is a rhombus but not a square. Find the area of rhombus.

Answer 1

Hint: In this question use the property that diagonals of rhombus are not of not equal length, thus to calculate the length of diagonal use the distance formula as coordinates of ends are given.

Complete step-by-step answer:

Proof –

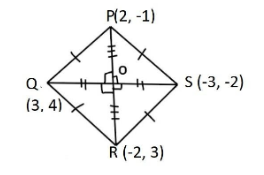
Points PQRS are shown above in a plane.
As we know that in a square and rhombus all the length of the sides are equal, but the length of diagonals are not equal in rhombus.
So as we know that the distance (d) between two points (x1, y1) and (x2, y2) is calculated as
$ \Rightarrow d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
So let $P = \left( {{x_1},{y_1}} \right) \equiv \left( {2, - 1} \right)$, $Q = \left( {{x_2},{y_2}} \right) \equiv \left( {3,4} \right)$, $R = \left( {{x_3},{y_3}} \right) \equiv \left( { - 2,3} \right)$, $S = \left( {{x_4},{y_4}} \right) \equiv \left( { - 3, - 2} \right)$
So the distance PQ $ = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} = \sqrt {{{\left( {3 - 2} \right)}^2} + {{\left( {4 + 1} \right)}^2}} = \sqrt {1 + 25} = \sqrt {26} $
Distance QR $ = \sqrt {{{\left( {{x_3} - {x_2}} \right)}^2} + {{\left( {{y_3} - {y_2}} \right)}^2}} = \sqrt {{{\left( { - 2 - 3} \right)}^2} + {{\left( {3 - 4} \right)}^2}} = \sqrt {25 + 1} = \sqrt {26} $
Distance RS $ = \sqrt {{{\left( {{x_4} - {x_3}} \right)}^2} + {{\left( {{y_4} - {y_3}} \right)}^2}} = \sqrt {{{\left( { - 3 + 2} \right)}^2} + {{\left( { - 2 - 3} \right)}^2}} = \sqrt {1 + 25} = \sqrt {26} $
Distance SP $ = \sqrt {{{\left( {{x_4} - {x_1}} \right)}^2} + {{\left( {{y_4} - {y_1}} \right)}^2}} = \sqrt {{{\left( { - 3 - 2} \right)}^2} + {{\left( { - 2 + 1} \right)}^2}} = \sqrt {25 + 1} = \sqrt {26} $
Distance PR $ = \sqrt {{{\left( {{x_3} - {x_1}} \right)}^2} + {{\left( {{y_3} - {y_1}} \right)}^2}} = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {3 + 1} \right)}^2}} = \sqrt {16 + 16} = \sqrt {32} = 4\sqrt 2 $
Distance QS $ = \sqrt {{{\left( {{x_4} - {x_2}} \right)}^2} + {{\left( {{y_4} - {y_2}} \right)}^2}} = \sqrt {{{\left( { - 3 - 3} \right)}^2} + {{\left( { - 2 - 4} \right)}^2}} = \sqrt {36 + 36} = \sqrt {72} = 6\sqrt 2 $
So as we see that all the sides are equal (i.e. PQ = QR = RS = SP = $\sqrt {26} $) but the length of diagonals are not equal.
The length of first diagonal PR = $4\sqrt 2 $ and the length of second diagonal QS = $6\sqrt 2 $.
Therefore it is a rhombus not a square.
The area of rhombus is given as ${\text{Area = }}\dfrac{{pq}}{2}$, where p is the length of one diagonal and q is the length of other diagonal.
$
   \Rightarrow {\text{Area = }}\dfrac{{PR \times QS}}{2} \\
   \Rightarrow \dfrac{{4\sqrt 2 \times 6\sqrt 2 }}{2} \\
   \Rightarrow 24sq{\text{ units}} \\
$
Hence proved.

Note: There are few more differences between a square and rhombus that could also have been used, the sides of a square are perpendicular to each other whereas the sides of a rhombus are not perpendicular to each other. All the angles of a square are equal however only opposite angles of a rhombus are equal. It is advised to remember the direct formula for the area of rhombus.