
If P is the point in the argand diagram corresponding to the complex number
Answer
427.8k+ views
1 likes
Hint: The argand diagram is used for graphical representation of complex numbers in the form of
Complete step-by-step solution:
The given complex number is;
According to the given question, let us draw the diagram to understand the question in a better way;
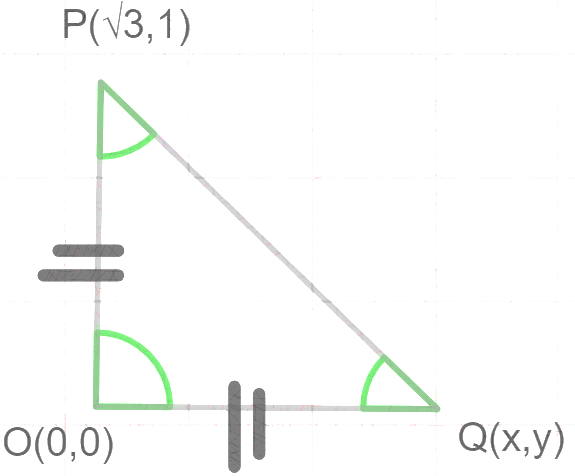
Figure
We know that if two lines are perpendicular to each other then the product of their slopes will be equal to
First, let us calculate the slope
Now, let us calculate slope
Put the respective values in the property
Simplifying the above equation;
Using the properties of isosceles triangles (stated in the note part) let us try to solve our question;
According to figure
By the distance formula between two points, we know that;
point and second point respectively )
Now, let us similarly find the equation for OQ;
Now, put the value of
The above equation can be further simplified as;
On comparing equation
Which means ;
Now put the value of
When
And
Therefore, there can be two possible values of
Therefore, the answer for this question is
Note: Here are the important properties of a right angled isosceles triangle. It will be easier to understand via a diagram, the isosceles triangle theorem states that;
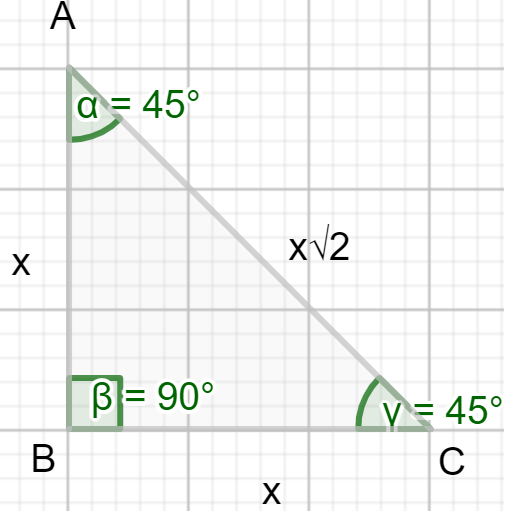
Figure
Complete step-by-step solution:
The given complex number is;
According to the given question, let us draw the diagram to understand the question in a better way;

Figure
We know that if two lines are perpendicular to each other then the product of their slopes will be equal to
First, let us calculate the slope
Now, let us calculate slope
Put the respective values in the property
Simplifying the above equation;
Using the properties of isosceles triangles (stated in the note part) let us try to solve our question;
According to figure
By the distance formula between two points, we know that;
point and second point respectively )
Now, let us similarly find the equation for OQ;
Now, put the value of
The above equation can be further simplified as;
On comparing equation
Which means ;
Now put the value of
When
And
Therefore, there can be two possible values of
Therefore, the answer for this question is
Note: Here are the important properties of a right angled isosceles triangle. It will be easier to understand via a diagram, the isosceles triangle theorem states that;

Figure
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Difference Between Prokaryotic Cells and Eukaryotic Cells

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Net gain of ATP in glycolysis a 6 b 2 c 4 d 8 class 11 biology CBSE

Give two reasons to justify a Water at room temperature class 11 chemistry CBSE




