Question

If p (1, 5), q (– 5, – 3) and r (x, y) are three points such that \[pr\bot rq\]. Find the equation of the circle that passes through p, q and r.

Answer 1

Hint: First we will find the unknown point (coordinates of r (x, y)) and then we will try to find out the center and radius of the circle using distance formula and then we will find the equation of the circle from the obtained data.
Distance formula, \[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
where d is the distance, \[\left( {{x}_{1}},{{y}_{1}} \right)\] are the coordinates of the first point and \[\left( {{x}_{2}},{{y}_{2}} \right)\] are the coordinates of the second point.

Complete step-by-step answer:
Given that p (1, 5), q (– 5, – 3) and r (x, y) are three points such that \[pr\bot rq\].

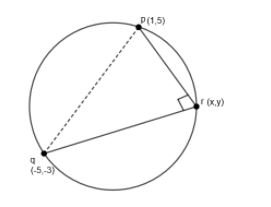
So, from the figure, it is clear that pqr is a right-angled triangle.
We have to find the equation of a circle passing through points p, q and r respectively.
First, we will try to find the coordinates of the point r (x, y).
We know that the general equation of the line is y = mx + c where m is the slope, y and x are the intercepts.
For finding the equation of a line between two points, we use
\[y=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)+c\]
(Neglect c as it is a constant)
\[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]
We have point p = (1, 5) and point r = (x, y).
Thus, slope \[\left( {{m}_{1}} \right)=\dfrac{y-5}{x-1}\]
Putting the value of slope in the general equation of the straight line, which is y = mx + c.
\[\Rightarrow y=\left( \dfrac{y-5}{x-1} \right)x+c\]
Put y = 5 and x = 1 in the general equation, we get
\[5=m\left( 1 \right)+c....\left( i \right)\]
Again put the value of m in the equation (i), we get
\[\Rightarrow 5=\left( \dfrac{y-5}{x-1} \right)\times 1\]
\[\Rightarrow 5\left( x-1 \right)=y-5\]
\[\Rightarrow 5x-5=y-5\]
\[\Rightarrow 5x-y-5=0....\left( ii \right)\]
Similarly, for points q and r,
we have, slope \[\left( {{m}_{2}} \right)=\dfrac{y-\left( -3 \right)}{x-\left( -5 \right)}\]
Put the value of x and y in the general equation of the straight line.
\[y=mx+c\]
\[-3=\left( {{m}_{2}} \right)\left( -5 \right)+c\]
Neglect c as it is a constant.
Here, the value of \[{{m}_{2}}\] in the equation (iii), we get
\[\Rightarrow -3=\left( \dfrac{y+3}{x+5} \right)\left( -5 \right)\]
\[\Rightarrow -3\left( x+5 \right)=-5\left( y+3 \right)\]
\[\Rightarrow -3x+5y-30=0\]
\[\Rightarrow 3x-5y+30=0.....\left( iv \right)\]
Solving equation (ii) and (iv), we get,
\[5x-y=5\]
\[3x-5y=-30\]
Multiply equation (ii), with 5 on both sides, we get,
\[25x-5y=25\]
Putting this value, we get
\[\begin{align}
  & 25x-5y=25 \\
 & 3x-5y=-30 \\
 & \underline{-\text{ + }} \\
 & 22x+0=55 \\
\end{align}\]
\[22x=55\]
\[x=\dfrac{55}{22}=2.5\]
Putting the value of x in equation (iv),
\[\Rightarrow 3\times 2.5-5y=-30\]
\[\Rightarrow 7.5-5y=-30\]
\[\Rightarrow -5y=-37.5\]
Multiplying both sides with (– 1), we get
\[\Rightarrow y=\dfrac{37.5}{5}=7.5\]
Now, we have three points as p (1, 5), q (– 5, – 3) and r (2.5, 7.5) which lie on the required circle.
Let us assume that the center of the circle is O having coordinates (h, k).
We know that radii of the circle are of equal length.
Thus, applying this property of the circle. We get,
\[po=qo=ro\]
These all are radii of the circle, thus, are of equal length.
Also, from the distance formula, we know that
\[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
where, d is the distance between two points.
Applying this between po and qo as both are radii of the same circle.
\[po=qo\]
\[\Rightarrow \sqrt{{{\left( h-1 \right)}^{2}}+{{\left( k-5 \right)}^{2}}}=\sqrt{h-{{\left( -5 \right)}^{2}}+{{\left( k-\left( -3 \right) \right)}^{2}}}\]
\[\Rightarrow \sqrt{{{h}^{2}}+{{1}^{2}}-2\left( h \right)\left( 1 \right)+{{k}^{2}}+{{5}^{2}}-2\left( 5 \right)\left( 10 \right)}=\sqrt{{{h}^{2}}+{{5}^{2}}+2\left( h \right)\left( 5 \right)+{{k}^{2}}+{{3}^{2}}+2\left( k \right)\left( 3 \right)}\]
\[\Rightarrow \sqrt{{{h}^{2}}+1-2h+{{k}^{2}}+25-10k}=\sqrt{{{h}^{2}}+25+10h+{{k}^{2}}+9+6k}\]
\[\Rightarrow \sqrt{{{h}^{2}}-2h+{{k}^{2}}-10k+26}=\sqrt{{{h}^{2}}+{{k}^{2}}+10h+6k+36}\]
On squaring both sides, we get
\[\Rightarrow {{h}^{2}}-2h+{{k}^{2}}-10k+26={{h}^{2}}+{{k}^{2}}+10h+6k+36\]
Canceling the like terms from both the sides, we get
\[\Rightarrow -2h-10k+26=10h+6k+36\]
\[\Rightarrow -2h-10k+26-10h-6k-36=0\]
\[\Rightarrow -12h-16k-10=0\]
Taking 2 common from both the sides, we get –
\[-6h-8k-5=0\]
Multiplying both sides with (– 1), we get,
\[6h+8k+5=0\]
\[6h+8k=-5....\left( v \right)\]
Similarly, for po = ro,
\[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
\[\Rightarrow \sqrt{{{\left( h-1 \right)}^{2}}+{{\left( k-5 \right)}^{2}}}=\sqrt{{{\left( h-2.5 \right)}^{2}}+{{\left( k-7.5 \right)}^{2}}}\]
\[\Rightarrow \sqrt{{{h}^{2}}+{{1}^{2}}-2\left( h \right)\left( 1 \right)+{{k}^{2}}+{{5}^{2}}-2\left( k \right)\left( 5 \right)}=\sqrt{{{h}^{2}}+{{\left( 2.5 \right)}^{2}}-2\left( 2.5 \right)\left( h \right)+{{k}^{2}}+{{\left( 7.5 \right)}^{2}}-2\left( k \right)\left( 7.5 \right)}\]
\[\Rightarrow \sqrt{{{h}^{2}}+1-2h+{{k}^{2}}+25-10k}=\sqrt{{{h}^{2}}+6.25-5h+{{k}^{2}}+56.25-15k}\]
Squaring both the sides, we get
\[\Rightarrow {{h}^{2}}+{{k}^{2}}-2h-10k+26={{h}^{2}}+{{k}^{2}}-5h-15k+62.5\]
Canceling the similar terms from both the sides we get
\[\Rightarrow -2h-10k+26=-5h-15k+62.5\]
\[\Rightarrow -2h+5h-10k+15k=62.5-26\]
\[\Rightarrow 3h+5k=36.5....\left( vi \right)\]
Solving equation (v) and (vi), we get
\[\begin{align}
  & 6h+8k=-5 \\
 & \underline{3h+5k=36.5} \\
\end{align}\]
Multiply equation (vi) with 2, we get
\[\begin{align}
  & 6h+8k=-5 \\
 & \underline{\begin{align}
  & 6h+10k=73 \\
 & - \\
\end{align}} \\
 & 0-2k=-78 \\
\end{align}\]
\[k=\dfrac{78}{2}=39\]
On putting the value of k = 39 in the equation (v), we get
\[6h+8\left( 39 \right)=-5\]
\[6h=-5-312\]
\[6h=-317\]
\[h=\dfrac{-317}{6}\]
\[h=-52.8\]
Now, we have h = – 52.8 and k = 39
\[\left( h,k \right)=\left( -52.8,39 \right)\]
We know that,
Radius of circle \[=\sqrt{{{h}^{2}}+{{k}^{2}}}\]
\[=\sqrt{{{\left( -52.8 \right)}^{2}}+{{\left( 39 \right)}^{2}}}\]
\[=\sqrt{2787.4+1521}\]
\[=65.6\]
We are ready with all the required values to form an equation of the circle.
We know that the general equation of the circle is
\[\Rightarrow {{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{\left( r \right)}^{2}}\]
\[\Rightarrow {{\left( x-\left( -52.8 \right) \right)}^{2}}+{{\left( y-39 \right)}^{2}}={{\left( 65.6 \right)}^{2}}\]
\[\Rightarrow {{\left( x+52.8 \right)}^{2}}+{{\left( y-39 \right)}^{2}}={{\left( 65.6 \right)}^{2}}\]
\[\Rightarrow {{x}^{2}}+{{\left( 52.8 \right)}^{2}}+2\left( x \right)\left( 52.8 \right)+{{y}^{2}}+{{\left( 39 \right)}^{2}}-2\left( y \right)\left( 39 \right)={{\left( 65.6 \right)}^{2}}\]’
\[\Rightarrow {{x}^{2}}+{{y}^{2}}+105x-78y={{\left( 65.6 \right)}^{2}}-{{\left( 65.6 \right)}^{2}}\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}+105x-78y=0\]
Thus, the required equation of the circle is \[{{x}^{2}}+{{y}^{2}}+105x-78y=0.\]

Note: As it is clearly given that pq perpendicular to rq, therefore, we can say \[{{m}_{1}}.{{m}_{2}}=-1\]. (Multiplication of two perpendicular slopes is always equal to – 1). From this relation of the slope, we will try to find the value of the unknown (h, k) and r then with the help of this, we will form the required equation of the circle. So, whenever we are faced with such questions, we can follow this approach so that it will save our time.