Question

If one of the zeros of the quadratic polynomial of the form \[{{x}^{2}}+ax+b\] is negative of the other, then it
(a) has no linear term and the constant term is negative
(b) has no linear term and the constant term is positive
(c) can have a linear term but the constant term is negative
(d) can have a linear term but the constant term is positive.

Answer 1

Hint: We will first write the general form of the quadratic equation as a product of linear terms containing their roots. Then we will put in the required conditions and obtain the answer.

Complete step-by-step answer:
Let us now begin with the solution.
There are three types of quadratic polynomials with the real roots. All of them are shown below.

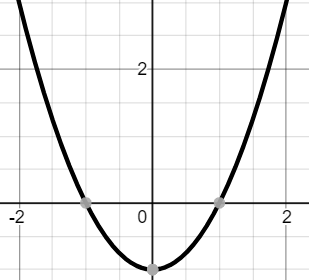
First type: one of the roots is negative

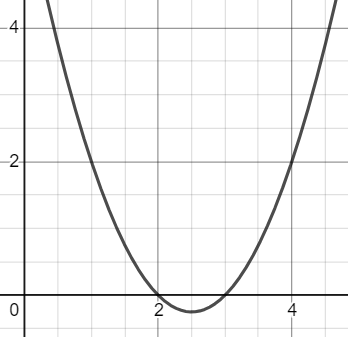
Second type: Both roots are positive

Third type: Both roots are negative
But in the question we deal with the polynomial which has one of the roots negative of the other.
Therefore, we deal with the first type.
Now we now that any quadratic polynomial can be written as a product of linear polynomials of their roots
\[{{x}^{2}}+ax+b=\left( x-p \right)\left( x-q \right)\] , where p and q are the zeros of the polynomial \[{{x}^{2}}+ax+b\] .
Now, as one of the roots is negative of the other let us assume the values of p and q.
Let p=a and let q=-a, where a is always a positive number.
Thus the equation becomes,
\[\begin{align}
  & {{x}^{2}}+ax+b=\left( x-a \right)\left( x-\left( -a \right) \right) \\
 & {{x}^{2}}+ax+b=\left( x-a \right)\left( x+a \right) \\
\end{align}\]
Multiplying we get,
\[{{x}^{2}}+ax+b=\left( x\times x \right)+\left( x\times a \right)+\left( -a\times x \right)+\left( -a\times a \right)\]
Taking out x as common, we get
\[{{x}^{2}}+ax+b={{x}^{2}}+x\left( a-a \right)-{{a}^{2}}\]
which means,
\[{{x}^{2}}+ax+b={{x}^{2}}+0x-{{a}^{2}}\]
Thus comparing we get b = 0 and c = -a2.
Thus the linear term becomes 0 and the constant term becomes negative.
Thus option(a) is correct.
Note: Please remember that a is always a positive number. If we take it to be any real number, then the constant term would become either positive or negative. Also, the linear would not become zero. Thus it will create a lot of confusion and our answer might go wrong.