Question

If one of the lines of $m{{y}^{2}}+\left( 1-{{m}^{2}} \right)xy-m{{x}^{2}}=0$ is a bisector of the angle between the line $xy=0$, then find the value of m?
(a) -2
(b) 1
(c) 2
(d) $\dfrac{-1}{2}$

Answer 1

Hint: We start solving the problem by finding the equation of lines present on the pairs of lines $m{{y}^{2}}+\left( 1-{{m}^{2}} \right)xy-m{{x}^{2}}=0$ and $xy=0$. We then find the angle between the lines present in $xy=0$ and find the slope of the line required to bisect the lines present in $xy=0$. We then equate this slope with the slopes of the lines present in $m{{y}^{2}}+\left( 1-{{m}^{2}} \right)xy-m{{x}^{2}}=0$ to get the required values of m.

Complete step-by-step solution
According to the problem, we are given that one of the lines of $m{{y}^{2}}+\left( 1-{{m}^{2}} \right)xy-m{{x}^{2}}=0$ is a bisector of the angle between the line $xy=0$.
Let us first find the lines present in the pair of lines $m{{y}^{2}}+\left( 1-{{m}^{2}} \right)xy-m{{x}^{2}}=0$.
So, we get $m{{y}^{2}}+xy-{{m}^{2}}xy-m{{x}^{2}}=0$.
$\Rightarrow y\left( my+x \right)-mx\left( my+x \right)=0$.
$\Rightarrow \left( y-mx \right)\left( my+x \right)=0$.
$\Rightarrow y-mx=0$ and $my+x=0$.
$\Rightarrow y=mx$ and $x=-my$ ---(1).
Now, let us find the lines present in the pair of lines \[xy=0\].
So, we get $x=0$ and $y=0$. We know that this represents both axes and the angle between them is ${{90}^{\circ }}$. In order to bisect both axes we need the lines that make ${{45}^{\circ }}$ with both x and y axes (assuming that the line bisects both axes in the first quadrant only).
So, the slope of the line should be $\tan \left( {{45}^{\circ }} \right)=1$.
Let us draw all the obtained information to get a better view.

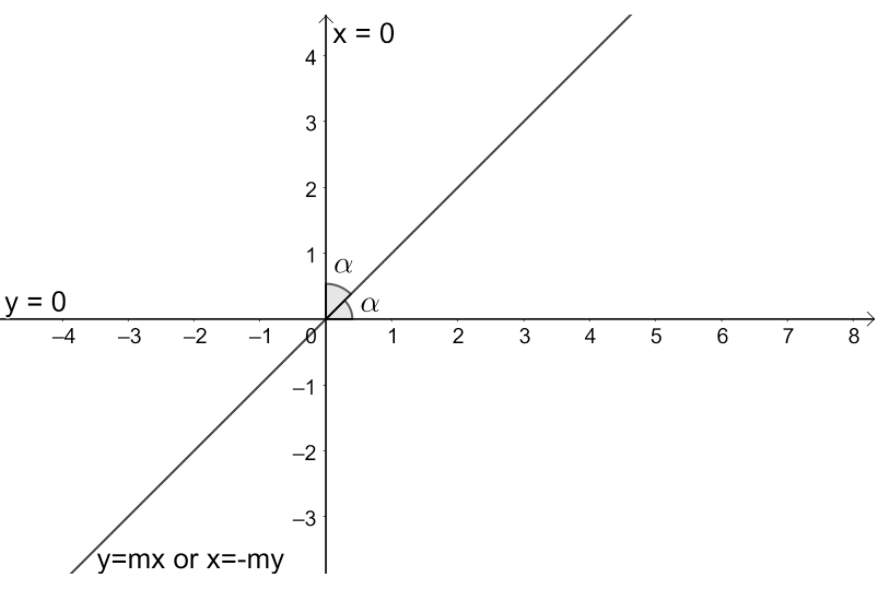
Let us assume that the line $y=mx$ is the bisector of lines $x=0$ and $y=0$. We know that the slope of the $y=mx+c$ is m. So, we get the value of m as 1 i.e., $m=1$ ---(2).
Now, let us assume that the line $x=-my$ is the bisector of lines $x=0$ and $y=0$.
So, we get $y=\dfrac{-1}{m}x$.
We know that the slope of the $y=mx+c$ is m.
So, we get the $\dfrac{-1}{m}=1$.
$\Rightarrow m=-1$ ---(3).
From equations (2) and (3), we have found that the values for “m” are 1 and –1.
∴ The correct option for the given problem is (b).

Note: We should know that the line making ${{135}^{\circ }}$ with x-axis will also bisect both x and y-axes but here we have taken an assumption that the angles lie in the first quadrant. Even if we take the slope of the line at the angle ${{135}^{\circ }}$, we get the same values for “m”. We should not make calculation mistakes while solving this problem. Similarly, we can expect problems to find the equation of the line that makes a triangle of area b which is formed when the line bisects both axes.