Question

If normal at the point $P\left( \theta \right)$ to the ellipse $\dfrac{{{x^2}}}{{14}} + \dfrac{{{y^2}}}{5} = 1$ , intersects it again at the point $Q\left( {2\theta } \right)$ , then $\cos \theta = $ ?

Answer 1

Hint:
We can write the parametric equation of points on the ellipse using the given angle. Then we can find their slope. Then we can find the equation of the normal in the parametric form. Then we can equate the two slopes. Then we can simplify the equation using trigonometric identities and find the required trigonometric ratio.

Complete step by step solution:

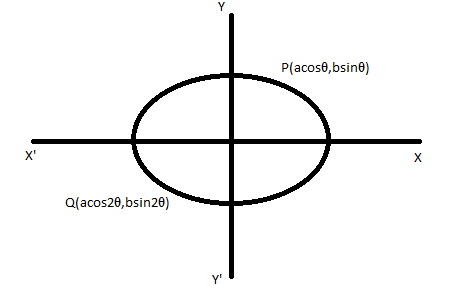
We are given the equation of the ellipse as $\dfrac{{{x^2}}}{{14}} + \dfrac{{{y^2}}}{5} = 1$ . On comparing with the standard equation of ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ , we can get the value of a and b.
 $ \Rightarrow {a^2} = 14$ and ${b^2} = 5$
We know that the point on an ellipse in the parametric form is given by $\left( {a\cos t,b\sin t} \right)$ .
So, we can write the given points P and Q in its parametric form as,
 $ \Rightarrow P\left( \theta \right) = \left( {a\cos \theta ,b\sin \theta } \right)$
 $ \Rightarrow Q\left( {2\theta } \right) = \left( {a\cos 2\theta ,b\sin 2\theta } \right)$
Now we can find the slope of the line joining the points P and Q.
We know that slope of the line joining 2 points is given by,
 $m = \dfrac{{{y_1} - {y_2}}}{{{x_1} - {x_2}}}$
On substituting the coordinates of the point, we get,
 $ \Rightarrow {m_1} = \dfrac{{b\sin 2\theta - b\sin \theta }}{{a\cos 2\theta - a\cos \theta }}$
We know that the slope of the normal is given by $\dfrac{a}{b}\tan \theta $
As the normal passes through the points P and Q, we can equate the slope.
 $ \Rightarrow \dfrac{{b\sin 2\theta - b\sin \theta }}{{a\cos 2\theta - a\cos \theta }} = \dfrac{a}{b}\tan \theta $
We know that $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$ . On applying this and taking the common factors, we get.
 $ \Rightarrow \dfrac{{b\left( {\sin 2\theta - \sin \theta } \right)}}{{a\left( {\cos 2\theta - \cos \theta } \right)}} = \dfrac{a}{b}\dfrac{{\sin \theta }}{{\cos \theta }}$
We know that $\sin 2A = 2\sin A\cos A$ and $\cos 2A = 2{\cos ^2}A - 1$
 $ \Rightarrow \dfrac{{b\left( {2\sin \theta \cos \theta - \sin \theta } \right)}}{{a\left( {2{{\cos }^2}\theta - 1 - \cos \theta } \right)}} = \dfrac{a}{b}\dfrac{{\sin \theta }}{{\cos \theta }}$
We can take sine outside the bracket and bring $\dfrac{a}{b}$ to the LHS. So, we get,
 $ \Rightarrow \dfrac{{{b^2}}}{{{a^2}}} \times \dfrac{{\sin \theta \left( {2\cos \theta - 1} \right)}}{{\left( {2{{\cos }^2}\theta - 1 - \cos \theta } \right)}} = \dfrac{{\sin \theta }}{{\cos \theta }}$
Now we can substitute the value of a and b and cancel the sin terms on both sides of the equation.
 $ \Rightarrow \dfrac{5}{{14}} \times \dfrac{{\left( {2\cos \theta - 1} \right)}}{{\left( {2{{\cos }^2}\theta - 1 - \cos \theta } \right)}} = \dfrac{1}{{\cos \theta }}$
On rearranging, we get,
 $ \Rightarrow \dfrac{5}{{14}} = \dfrac{{\left( {2{{\cos }^2}\theta - 1 - \cos \theta } \right)}}{{\cos \theta \left( {2\cos \theta - 1} \right)}}$
On cross- multiplying, we get,
 $ \Rightarrow 5\cos \theta \left( {2\cos \theta - 1} \right) = 14\left( {2{{\cos }^2}\theta - 1 - \cos \theta } \right)$
On opening the brackets, we get,
 $ \Rightarrow 10{\cos ^2}\theta - 5\cos \theta = 28{\cos ^2}\theta - 14 - 14\cos \theta $
On rearranging, we get,
 $ \Rightarrow 28{\cos ^2}\theta - 10{\cos ^2}\theta - 14\cos \theta + 5\cos \theta - 14 = 0$
On adding like terms, we get,
 $ \Rightarrow 18{\cos ^2}\theta - 9\cos \theta - 14 = 0$
Now we can split the middle term
 $ \Rightarrow 18{\cos ^2}\theta - 21\cos \theta + 12\cos \theta - 14 = 0$
On taking the common factors, we get,
 $ \Rightarrow 3\cos \theta \left( {6\cos \theta - 7} \right) + 2\left( {6\cos \theta - 7} \right) = 0$
Again, on taking the common terms, we get,
 $ \Rightarrow \left( {3\cos \theta + 2} \right)\left( {6\cos \theta - 7} \right) = 0$
When $\left( {6\cos \theta - 7} \right) = 0$ ,
 $ \Rightarrow 6\cos \theta = 7$
On dividing throughout with 6, we get,
 $ \Rightarrow \cos \theta = \dfrac{7}{6}$ This value of cos is not possible as its value cannot be greater than 1.
 When $\left( {3\cos \theta + 2} \right) = 0$
On rearranging, we get,
 $ \Rightarrow 3\cos \theta = - 2$
On dividing throughout with 3, we get,
 $ \Rightarrow \cos \theta = \dfrac{{ - 2}}{3}$

So, the required value of $\cos \theta $ is equal to $\dfrac{{ - 2}}{3}$.

Note:
Alternate solution to this problem is given by,
We are given the equation of the ellipse as $\dfrac{{{x^2}}}{{14}} + \dfrac{{{y^2}}}{5} = 1$ . On comparing with the standard equation of ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ , we can get the value of a and b.
 $ \Rightarrow {a^2} = 14$ and ${b^2} = 5$
We know that the point on an ellipse in the parametric form is given by $\left( {a\cos t,b\sin t} \right)$ .
So, we can write the given points P and Q in its parametric form as,
 $ \Rightarrow P\left( \theta \right) = \left( {a\cos \theta ,b\sin \theta } \right)$
 $ \Rightarrow Q\left( {2\theta } \right) = \left( {a\cos 2\theta ,b\sin 2\theta } \right)$
We know that equation of the normal to the point $\left( {{x_0},{y_0}} \right)$ is given by \[\dfrac{{{a^2}x}}{{{x_0}}} - \dfrac{{{b^2}y}}{{{y_0}}} = {a^2} - {b^2}\] .
On substituting the coordinates of the point P, we get,
 \[ \Rightarrow \dfrac{{{a^2}x}}{{a\cos \theta }} - \dfrac{{{b^2}y}}{{b\sin \theta }} = {a^2} - {b^2}\]
On simplification, we get,
 \[ \Rightarrow \dfrac{{ax}}{{\cos \theta }} - \dfrac{{by}}{{\sin \theta }} = {a^2} - {b^2}\]
It is given that point Q lines on the normal. So, its coordinates satisfy the equations on the normal.
 \[ \Rightarrow \dfrac{{a \times a\cos 2\theta }}{{\cos \theta }} - \dfrac{{b \times b\sin 2\theta }}{{\sin \theta }} = {a^2} - {b^2}\]
We know that $\sin 2A = 2\sin A\cos A$ and $\cos 2A = 2{\cos ^2}A - 1$
 \[ \Rightarrow \dfrac{{{a^2} \times \left( {2{{\cos }^2}\theta - 1} \right)}}{{\cos \theta }} - \dfrac{{{b^2} \times 2\sin \theta \cos \theta }}{{\sin \theta }} = {a^2} - {b^2}\]
Now we can substitute the value of a and b and cancel the common terms
 \[ \Rightarrow \dfrac{{14\left( {2{{\cos }^2}\theta - 1} \right)}}{{\cos \theta }} - 5 \times 2\cos \theta = 14 - 5\]
On multiplying throughout with \[\cos \theta \] , we get,
 \[ \Rightarrow 28{\cos ^2}\theta - 14 - 10{\cos ^2}\theta = 9\cos \theta \]
On rearranging, we get,
 $ \Rightarrow 18{\cos ^2}\theta - 9\cos \theta - 14 = 0$
Now we can split the middle term
 $ \Rightarrow 18{\cos ^2}\theta - 21\cos \theta + 12\cos \theta - 14 = 0$
On taking the common factors, we get,
 $ \Rightarrow 3\cos \theta \left( {6\cos \theta - 7} \right) + 2\left( {6\cos \theta - 7} \right) = 0$
Again, on taking the common terms, we get,
 $ \Rightarrow \left( {3\cos \theta + 2} \right)\left( {6\cos \theta - 7} \right) = 0$
When $\left( {6\cos \theta - 7} \right) = 0$ ,
 $ \Rightarrow 6\cos \theta = 7$
On dividing throughout with 6, we get,
 $ \Rightarrow \cos \theta = \dfrac{7}{6}$ This value of cos is not possible as its value cannot be greater than 1.
 When $\left( {3\cos \theta + 2} \right) = 0$
On rearranging, we get,
 $ \Rightarrow 3\cos \theta = - 2$
On dividing throughout with 3, we get,
 $ \Rightarrow \cos \theta = \dfrac{{ - 2}}{3}$
So, the required value of $\cos \theta $ is equal to $\dfrac{{ - 2}}{3}$ .