Question

If \[\left( {{x}_{1}},{{y}_{1}} \right)\] and $\left( {{x}_{2}},{{y}_{2}} \right)$ are the endpoints of a focal chord of the parabola ${{y}^{2}}=5x$, then find the value of $4{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}$?
A. $25$
B. $5$
C. $0$
D. $\dfrac{5}{4}$

Answer 1

Hint: First we will start with defining what is a focal chord then we will assume one endpoint of a focal chord on the standard parabola that is ${{y}^{2}}=4ax$ and then derive the second endpoint. After that we will compare the given equation of the parabola in the question and compare it with the ${{y}^{2}}=4ax$ and find the value of a and then compare the given endpoints to the derived ones and then put it in the $4{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}$ to get the answer.

Complete step by step answer:
We know that the chord of the parabola which passes through the focus is called the focal chord or in other words, any chord to ${{y}^{2}}=4ax$.which passes through the focus is called a focal chord of the parabola ${{y}^{2}}=4ax$.
Let ${{y}^{2}}=4ax$ be the equation of a parabola and $\left( a{{t}^{2}},2at \right)$ a point $P$ on it , suppose the coordinates of the other end is $Q$ of the focal chord passing through the focal point $S\left( a,0 \right)$ are $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)$. Now $PS$ and $SQ$ have the same slopes
$\begin{align}
  & \Rightarrow \dfrac{\left( 2a-0 \right)}{\left( a{{t}^{2}}-a \right)}=\dfrac{\left( 2a{{t}_{1}}-0 \right)}{\left( a{{t}_{1}}^{2}-a \right)}\Rightarrow t{{t}_{1}}^{2}-t={{t}_{1}}{{t}^{2}}-{{t}_{1}} \\
 & \Rightarrow \left( t{{t}_{1}}+1 \right)\left( {{t}_{1}}-t \right)=0 \\
 & \Rightarrow {{t}_{1}}=\dfrac{-1}{t} \\
\end{align}$
Hence the other end point $Q\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)\Rightarrow Q\left( \dfrac{a}{{{t}^{2}}},\dfrac{-2a}{t} \right)$ as shown in the figure below:

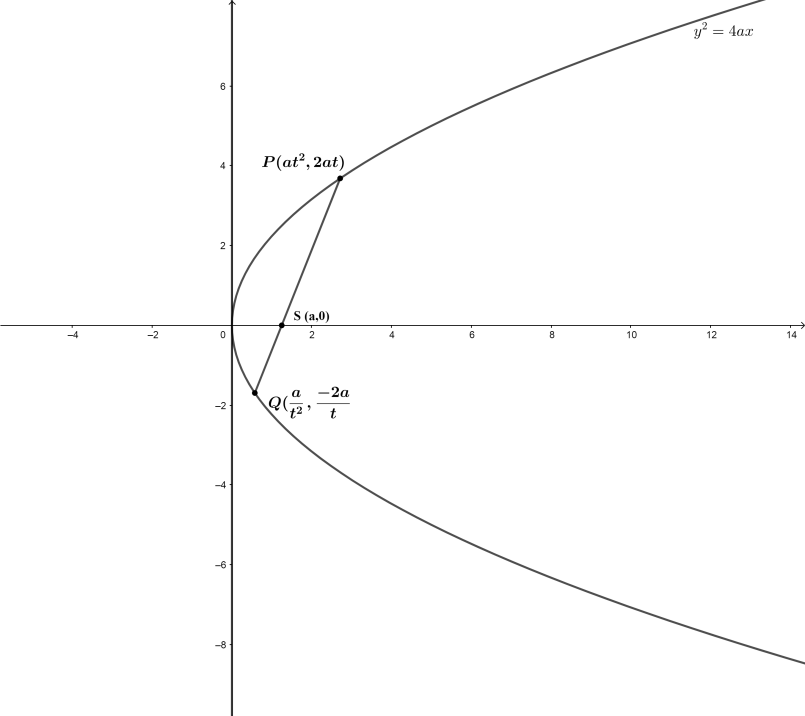
Now we are given the parabolic equation as follows: ${{y}^{2}}=5x$, and \[\left( {{x}_{1}},{{y}_{1}} \right)\] and $\left( {{x}_{2}},{{y}_{2}} \right)$ as the endpoints of a focal chord of the given parabola.
Let’s draw this information on a graph, we will mark the endpoints as follows:
\[P\left( {{x}_{1}},{{y}_{1}} \right)\] and $Q\left( {{x}_{2}},{{y}_{2}} \right)$ ,
Now let the focus of the parabola be $S\left( a,0 \right)$ :

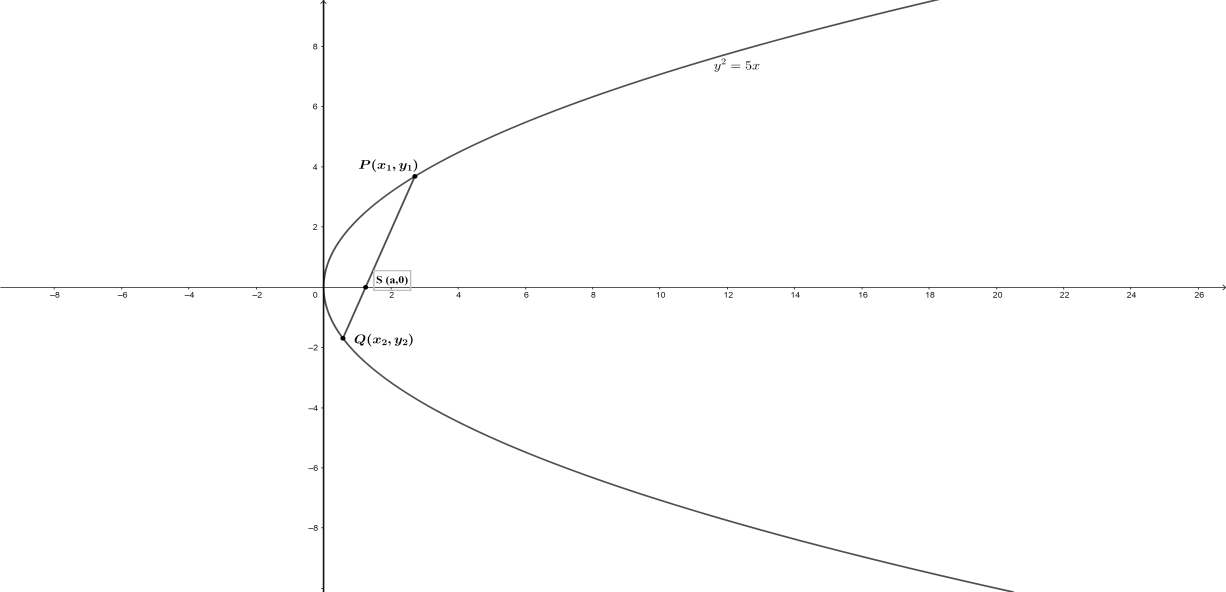
First, let’s find out the focal point that is $S\left( a,0 \right)$ , for that we have to find the value of $a$ , now we know that $a$ here stands for the value from the standard equation of the parabola that is ${{y}^{2}}=4ax$.
 We are given${{y}^{2}}=5x$ in the question now let’s compare it with the standard equation of parabola that is ${{y}^{2}}=4ax$, so we can see that: $4a=5\Rightarrow a=\dfrac{5}{4}$ .
Therefore, the focal point will be: $S\left( \dfrac{5}{4},0 \right)$
Now as we saw above in the derivation that the endpoints of a parabola are in the form of:
$P\left( a{{t}^{2}},2at \right)$ and $Q\left( \dfrac{a}{{{t}^{2}}},\dfrac{-2a}{t} \right)$ and we have the value of $a$ as $\dfrac{5}{4}$ , therefore the endpoints of our parabola will be in the following form:
$P\left( \left( \dfrac{5}{4} \right){{t}^{2}},2\left( \dfrac{5}{4} \right)t \right)\Rightarrow P\left( \dfrac{5{{t}^{2}}}{4},\dfrac{5t}{2} \right)$ and $Q\left( \dfrac{5}{4{{t}^{2}}},\dfrac{-2.5}{4t} \right)\Rightarrow Q\left( \dfrac{5}{4{{t}^{2}}},\dfrac{-5}{2t} \right)$
Now we have the endpoints \[P\left( {{x}_{1}},{{y}_{1}} \right)\] and $Q\left( {{x}_{2}},{{y}_{2}} \right)$ , from the question we will now compare both the values and find the values of ${{x}_{1}},{{y}_{1}},{{x}_{2}},{{y}_{2}}$ .
\[P\left( {{x}_{1}},{{y}_{1}} \right)=P\left( \dfrac{5{{t}^{2}}}{4},\dfrac{5t}{2} \right)\Rightarrow {{x}_{1}}=\dfrac{5{{t}^{2}}}{4},\text{ }{{y}_{1}}=\dfrac{5t}{2}\]
\[Q\left( {{x}_{2}},{{y}_{2}} \right)=q\left( \dfrac{5}{4{{t}^{2}}},\dfrac{-5}{2t} \right)\Rightarrow {{x}_{2}}=\dfrac{5}{4{{t}^{2}}},\text{ }{{y}_{2}}=\dfrac{-5}{2t}\]
Now, it is asked in the question to find the value of $4{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}$ , we will put the values of ${{x}_{1}},{{y}_{1}},{{x}_{2}},{{y}_{2}}$ :
$\begin{align}
  & \Rightarrow 4{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}=4\left( \dfrac{5{{t}^{2}}}{4}\times \dfrac{5}{4{{t}^{2}}} \right)+\left( \dfrac{5t}{2}\times \dfrac{-5}{2t} \right)=4\left( \dfrac{25}{16} \right)-\left( \dfrac{25}{4} \right) \\
 & \Rightarrow 4{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}=\left( \dfrac{25}{4} \right)-\left( \dfrac{25}{4} \right)=0 \\
 & \Rightarrow 4{{x}_{1}}{{x}_{2}}+{{y}_{1}}{{y}_{2}}=0 \\
\end{align}$
Hence, the answer is option C.
Note:
Students might make the mistake while finding the value of $a$ as one may directly take the coefficient of $x$ as the value of $a$. Always remember to divide it by $4$ and then get the value of $a$. We have taken $P$ as $\left( a{{t}^{2}},2at \right)$ because every point on the parabola will be in this format only where $t$ is any variable.