Question

If ‘l’ is any given line and P is a point not lying on l, then the number of parallel lines that can be drawn through P, parallel to l would be:
(a) One
(b) Two
(c) Infinite
(d) None of these

Answer 1

Hint: Draw any line ‘l’ and take any point P, not on the line. Draw all the possible lines passing through P. Consider only those lines which are parallel to the line ‘l’. Count the number of such lines to get the number of lines passing through a point which are parallel to the given line.

Step-by-step answer:
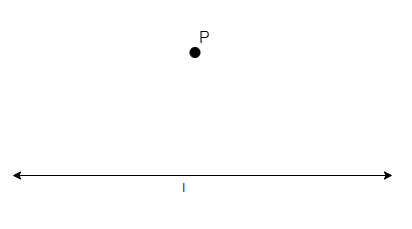
We have a line ‘l’ and a point P not lying on the line. We have to count the number of lines passing through this point which are parallel to the given line.
To do so, we will draw a line ‘l’, as shown in the figure.

We will now take a point P outside the line ‘l’.

We will draw a line passing through point P, as shown in the figure.

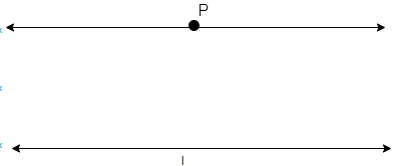
We observe that we can draw multiple lines passing through any point. However, we can draw only one line passing through a point that is parallel to line ‘l’.
Hence, the number of lines that can pass through a point parallel to a line is one, which is option (a).

Note: Keep in mind that we have to draw a line parallel to the given line. Two lines are said to be parallel when they never intersect with each other. If we consider any other line passing through point P, it won’t be parallel to line ‘l’.