Question

If l and l’ are the lengths of segment of focal chord of a parabola \[{{y}^{2}}=4ax\], then prove that \[\dfrac{1}{l}+\dfrac{1}{l'}=\dfrac{1}{a}\].

Answer 1

Hint: In the above question we will use the parametric form of the parabola \[{{y}^{2}}=4ax\] which is \[\left( a{{t}^{2}},2at \right)\]. We will use the property of a focal chords, if one end of a focal chord A \[=\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)\] and the other end of a focal chord B \[=\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)\] then \[{{t}_{1}}{{t}_{2}}=-1\].

Complete step-by-step answer:
We will also use the distance formula between two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] as follows:
Distance \[=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}\]

We have been given a parabola \[{{y}^{2}}=4ax\] and l and l’ are the lengths of segment of focal chord of parabola and then we have to prove \[\dfrac{1}{l}+\dfrac{1}{l'}=\dfrac{1}{a}\].
We know the parametric form of the parabola \[{{y}^{2}}=4ax\] is \[\left( a{{t}^{2}},2at \right)\].
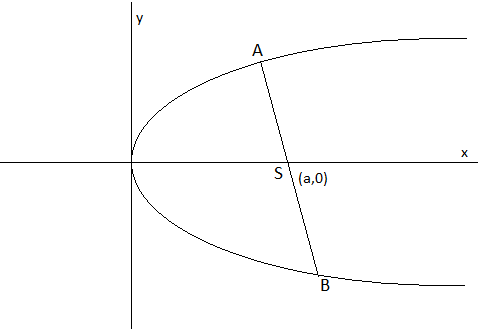
Let us suppose the end points of focal chord A \[\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right)\] and the other end point B \[\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)\].
By the property of focal chords we know that \[{{t}_{1}}{{t}_{2}}=-1\]
\[\Rightarrow {{t}_{2}}=\dfrac{-1}{{{t}_{1}}}\]
On substituting the value of \[{{t}_{2}}\] in point B, we get as follows:
\[\begin{align}
  & a{{t}_{2}}^{2}=a{{\left( \dfrac{-1}{{{t}_{1}}} \right)}^{2}}=\dfrac{a}{{{t}_{1}}^{2}} \\
 & 2a{{t}_{2}}=2a\left( \dfrac{-1}{{{t}_{1}}} \right)=\dfrac{-2a}{{{t}_{1}}} \\
\end{align}\]
So the point B is \[\left( \dfrac{a}{{{t}_{1}}^{2}},\dfrac{-2a}{{{t}_{1}}} \right)\].
Also, focus is S = (a,0)

We know the distance formula between two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] as follows:
Distance \[=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}\]
By using the distance formula the length of segment of focal chords are as follows:
\[l=AS=\sqrt{{{\left( a{{t}_{1}}^{2}-a \right)}^{2}}+{{\left( 2a{{t}_{1}} \right)}^{2}}}\]
Using the identity \[{{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\] in the above equation, we get as follows:
\[\begin{align}
  & \Rightarrow \sqrt{{{a}^{2}}{{\left( {{t}_{1}}^{2}-1 \right)}^{2}}+4{{a}^{2}}{{t}_{1}}^{2}} \\
 & \Rightarrow \sqrt{{{a}^{2}}{{t}_{1}}^{4}-2{{a}^{2}}{{t}_{1}}^{2}+{{a}^{2}}+4{{a}^{2}}{{t}_{1}}^{2}} \\
 & \Rightarrow \sqrt{{{a}^{2}}{{t}_{1}}^{4}+2{{a}^{2}}{{t}_{1}}^{2}+{{a}^{2}}} \\
 & \Rightarrow \sqrt{{{a}^{2}}{{\left( {{t}_{1}}^{2}+1 \right)}^{2}}} \\
 & \Rightarrow a\left( {{t}_{1}}^{2}+1 \right) \\
\end{align}\]
\[l'=BS=\sqrt{{{\left( \dfrac{a}{{{t}_{1}}^{2}}-a \right)}^{2}}+{{\left( \dfrac{-2a}{{{t}_{1}}}-0 \right)}^{2}}}\]
Using the identity \[{{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}\] in the above equation, we get as follows:
\[\begin{align}
  & \Rightarrow \sqrt{\dfrac{{{a}^{2}}}{{{t}_{1}}^{4}}-\dfrac{2{{a}^{2}}}{{{t}_{1}}^{2}}+{{a}^{2}}+\dfrac{4{{a}^{2}}}{{{t}_{1}}^{2}}} \\
 & \Rightarrow \sqrt{\dfrac{{{a}^{2}}}{{{t}_{1}}^{4}}+\dfrac{2{{a}^{2}}}{{{t}_{1}}^{2}}+{{a}^{2}}} \\
 & \Rightarrow \sqrt{{{\left( \dfrac{a}{{{t}_{1}}^{2}}+a \right)}^{2}}} \\
 & \Rightarrow \dfrac{a}{{{t}_{1}}^{2}}+a=a\left( \dfrac{1}{{{t}_{1}}^{2}}+1 \right) \\
 & \Rightarrow \dfrac{a\left( 1+{{t}_{1}}^{2} \right)}{{{t}_{1}}^{2}} \\
\end{align}\]
Now, \[\dfrac{1}{l}+\dfrac{1}{l'}=\dfrac{1}{a\left( {{t}_{1}}^{2}+1 \right)}+\dfrac{{{t}_{1}}^{2}}{a\left( {{t}_{1}}^{2}+1 \right)}\]
Taking \[\dfrac{1}{a\left( {{t}_{1}}^{2}+1 \right)}\] as common we get as follows:
\[\Rightarrow \dfrac{1}{a\left( {{t}_{1}}^{2}+1 \right)}\left[ 1+{{t}_{1}}^{2} \right]=\dfrac{1}{a}\]
Hence, it is proved that \[\dfrac{1}{l}+\dfrac{1}{l'}=\dfrac{1}{a}\].

Note: Be careful while doing calculation as there is a chance that you might make a sign mistake while using the distance formula as well as finding the value of ‘\[{{t}_{2}}\]’ in terms of ‘\[{{t}_{1}}\]’ by using the property of focal chord. Also remember that a focal chord means the chord that passes through the focus of the parabola.