Question

If it costs Rs. $$160$$ to carpet a square room $$8$$ metres broad, what would it cost at the same rate per square metre to carpet an oblong room $$6$$ metre by $$5$$ metre?

Answer 1

Hint: It is given that the room is square. The cost to carpet that square room is mentioned. We need to find the cost of carpeting a similar room at the same cost. So we will use the cross multiplication method to solve for the unknown. We will find the total area of both the rooms. Then cross multiply to find the cost for the given room.
The formulas used to solve the problem are:
Area of a square, $${A_{sq}} = {a^2}$$
Where, $$a$$ is the length of the side of the square.
Area of rectangle, $${A_{rect}} = l \times b$$
Where, $$l$$ is the length and $$b$$ is the breadth of the rectangle.

Complete answer:
Let us consider the square room, which is as follows,

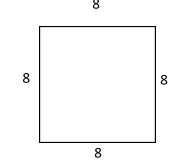
Now, let us find out the area of the square,
$$\eqalign{
  & \Rightarrow {A_{sq}} = {8^2} \cr
  & \Rightarrow {A_{sq}} = 64{m^2} \cr} $$
Let us consider the oblong room, which by seeing the dimensions is a rectangle,

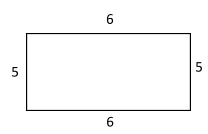
The area of this rectangle is given by,
$$\eqalign{
  & \Rightarrow {A_{rect}} = 6 \times 5 \cr
  & \Rightarrow {A_{rect}} = 30{m^2} \cr} $$
Now, we can write the relation of given and to find as like this,
$$\eqalign{
  & 64{m^2} = Rs.160 \cr
  & 30{m^2} = x \cr} $$
Now we solve for $$x$$ by cross multiplying,
$$ \Rightarrow x \times 64 = 30 \times 160$$
$$ \Rightarrow x = \dfrac{{4800}}{{64}}$$
$$ \Rightarrow x = Rs.75$$
The final answer is $$Rs.75$$.

Note:
This is one of the simplest methods to solve these kinds of problems. Make sure that you find the area of both the given rooms. Remember that the units in LHS and RHS should be the same for cross-multiplying. Also, do not forget the units, area is expressed as square units. And after cross multiplying, use the proper unit for the unknown quantity.