Question

If in triangle ∆PQR, sin P, sin Q, sin R are in Arithmetic Progression (AP). Then,

\[
  {\text{A}}{\text{. The altitudes are in AP}} \\
  {\text{B}}{\text{. The altitudes are in HP}} \\
  {\text{C}}{\text{. The medians are in GP}} \\
  {\text{D}}{\text{. The medians are in AP}} \\
\]

Answer 1

Hint – To determine the answer we write the area of the triangle in terms of sides and altitudes. Then we use Sine rule on them.

Complete Step-by-Step solution:
Let a, b, c be the sides of the triangle PQR respectively.
Let $p_1, p_2, p_3$ be the altitudes of the respective sides of the triangle.

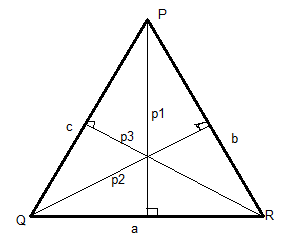
We know, the sine rule in a triangle states,
$\dfrac{{\text{a}}}{{{\text{SinP}}}}$ = $\dfrac{{\text{b}}}{{{\text{SinQ}}}}$ = $\dfrac{{\text{c}}}{{{\text{SinR}}}}$ = k (constant) -- (1)

We know that,

Area of the triangle (A)​= $\dfrac{1}{2}$ x length of side x length of altitude = $\dfrac{1}{2}$bh
                                                                                                                  = $\dfrac{1}{2}.a.p_1$
                                                = $\dfrac{1}{2}.b.p_2$
                                                 = $\dfrac{1}{2}.c.p_3$
⟹2 (Area of triangle) = 2A =a × $p_1$
⟹$p_1$ = $\dfrac{{2{\text{A}}}}{{\text{a}}} = \dfrac{{{\text{2A}}}}{{{\text{k SinP}}}}$ --- from (1)
Similarly, $p_2$ = $\dfrac{{{\text{2A}}}}{{{\text{k SinQ}}}}$and p3 = $\dfrac{{{\text{2A}}}}{{{\text{k SinR}}}}$

Given Data: sin P, sin Q, sin R are in AP
We know that if the elements of a series are in AP, then their reciprocals are in HP.
Therefore,$\dfrac{1}{{{\text{SinP}}}}$, $\dfrac{1}{{{\text{SinQ}}}}$and $\dfrac{1}{{{\text{SinR}}}}$are in HP.
We multiply it with 2A,
⟹$\dfrac{{{\text{2A}}}}{{{\text{SinP}}}}$, $\dfrac{{{\text{2A}}}}{{{\text{SinQ}}}}$and $\dfrac{{{\text{2A}}}}{{{\text{SinR}}}}$are in HP.

As Area of the triangle is directly proportional to the altitude, we can say
$p_1, p_2$ and $p_3$ are in HP.

Hence, all the altitudes are in HP. Option B is the correct answer.

Note: In order to solve such types of problems the key is to write the area of the triangle in terms of sides and altitudes and using the Sine rule. We should know the relation between AP and HP. HP stands for Harmonic mean which is one of several kinds of average, and in particular, one of the Pythagorean means and is the inverse of AP.