Question

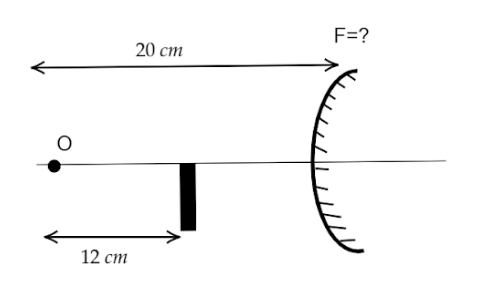
If images formed by both mirrors coincide then what is the focal length of a convex mirror?

A. $5\,cm$
B. $10\,cm$
C. $15\,cm$
D. $20\,cm$

Answer 1

Hint: In this question that distance of the object placed is given. It is stated that the image formed from the plane mirror coincides with the concave mirror. The distance between the object from the plane mirror and image from the plane mirror are equal. Hence, by using this and substituting in a mirror formula we will find the answers.

Complete step by step answer:
Let us first come to the part of the plane mirror.
The object is at a distance of $12{\text{ }}cm$ from the plane mirror.
As we know that the object distance and image distance from a plane mirror are equal.
So, the image formed from the plane mirror is at a distance $12{\text{ }}cm$ from the mirror.

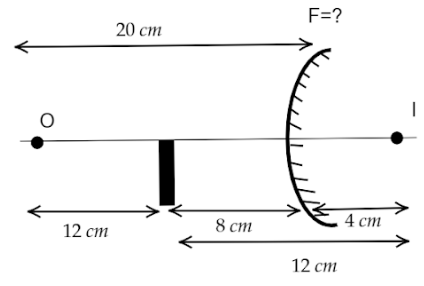
Now, the distance between the plane mirror and the concave mirror is $\left( {20 - 12} \right) = 8{\text{ }}cm$. Now, as the image has formed $12{\text{ }}cm$ from the plane mirror implies that the image has formed $\left( {12 - 8} \right) = 4cm$ to the right of the concave mirror.According to the question, both the images formed from the mirror coincides, which means that the image forms $4cm$ from the concave mirror.

In case of concave mirror, by using mirror signs,
Object distance$ = u = - 20{\text{ }}cm$
Image distance$ = v = + 4{\text{ }}cm$
Let the focal length of the concave mirror be $f$.
Thus, from mirror formula we get,
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Substituting the values we get,
$\dfrac{1}{4} - \dfrac{1}{{20}} = \dfrac{1}{f}$
Solving the equation we get,
$\therefore f = 5\,{\text{ }}cm$.
So, the focal length of the mirror is $5\,cm$.

Hence, the correct option is A.

Note: It must be noted that the sign convention for the mirror is taken as that the distance right to the pole and upwards the principle axis is considered as positive whereas anything left to the pole and downwards the principle axis is considered as negative. The focal length of a plane mirror is infinity.