Question

If I is the incentre of triangle ABC and AI when produced meets the circumcircle of triangle ABC in point D. If $\angle BAC = 66^\circ $and $\angle ABC = 80^\circ $. Calculate $\angle BIC$.

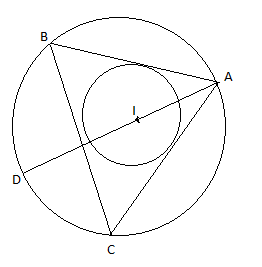
Answer 1

Hint: Incentre of the triangle can be defined as the point at which all the three bisectors of the triangle meet that intersect. It is also known as the center of the triangle’s incircle which is the largest circle that can fit the triangle inside it.

Complete step by step solution:
Take the given diagram and combine point B and D , D and C, B and I and I and B as shown in the figure.

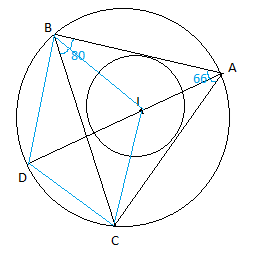
Here, we can observe that $\angle DBC$ and $\angle DAC$ are in the same segment.
$\angle DBC = \angle DAC$ ….. (I)
But, by using the bisectors concept
$\angle DAC = \dfrac{1}{2}\angle BAC$
Place the given values in the above equation –
$\angle DAC = \dfrac{1}{2} \times 66$
Common factors from the numerator and the denominator cancel each other.
$\angle DAC = 33^\circ $
Place above values in the equation (I)
$\angle DAC = \angle DBC = 33^\circ $ …. (II)
Since, we can observe that I is the incentre of the given triangle. IB bisects $\angle ABC$
$\angle IBC = \dfrac{1}{2}\angle ABC$
Place the value of the given angle –
$\angle IBC = \dfrac{1}{2} \times 80^\circ $
Common factors from the numerator and the denominator cancel each other.
$\angle IBC = 40^\circ $
Now, in triangle ABC $\angle BAC = 66^\circ $and $\angle ABC = 80^\circ $
In $\Delta ABC,{\text{ }}\angle {\text{ACB = 180}}^\circ {\text{ - (}}\angle {\text{ABC + }}\angle {\text{BAC)}}$
Place the values –
$
  \angle {\text{ACB = 180}}^\circ {\text{ - (80}}^\circ {\text{ + 66}}^\circ {\text{)}} \\
  \angle {\text{ACB = 180}}^\circ {\text{ - (156}}^\circ {\text{)}} \\
  \angle {\text{ACB = 34}}^\circ \\
 $
Similarly, IC bisects the angle C
$
  \angle ICB = \dfrac{1}{2}\angle C = \dfrac{1}{2} \times 34^\circ \\
  \angle ICB = 17^\circ \\
 $
Now, in triangle IBC,
$\angle IBC + \angle ICB + \angle BIC = 180^\circ $
Place all the known values in the given equation –
\[
  40^\circ + 17^\circ + \angle BIC = 180^\circ \\
  57^\circ + \angle BIC = 180^\circ \\
  \angle BIC = 180^\circ - 57^\circ \\
  \angle BIC = 123^\circ \\
 \]
Hence, the required angle is \[\angle BIC = 123^\circ \].

Note:
Always remember the sum of all the three angles in the triangle is always one hundred and eighty degrees. Be careful when you make the required angle the subject, when terms are moved to the opposite side, the sign of the term is changed positive to negative and vice-versa.