Question

If height of a cone is h, its slant height is l, then radius of its base will be,
A. $\sqrt{l+h}$
B. $\sqrt{l-h}$
C. $\sqrt{{{h}^{2}}-{{l}^{2}}}$
D. $\sqrt{{{l}^{2}}-{{h}^{2}}}$

Answer 1

Hint: We will first start by drawing a rough sketch of the cone and then mark all its dimensions as given to us. Then we will apply the Pythagoras Theorem in the right angle formed by the slant height of the cone to find the radius.

Complete step-by-step answer:
Now, we have been given a cone with height h and slant height l. Now, we let the radius of the cone be r.

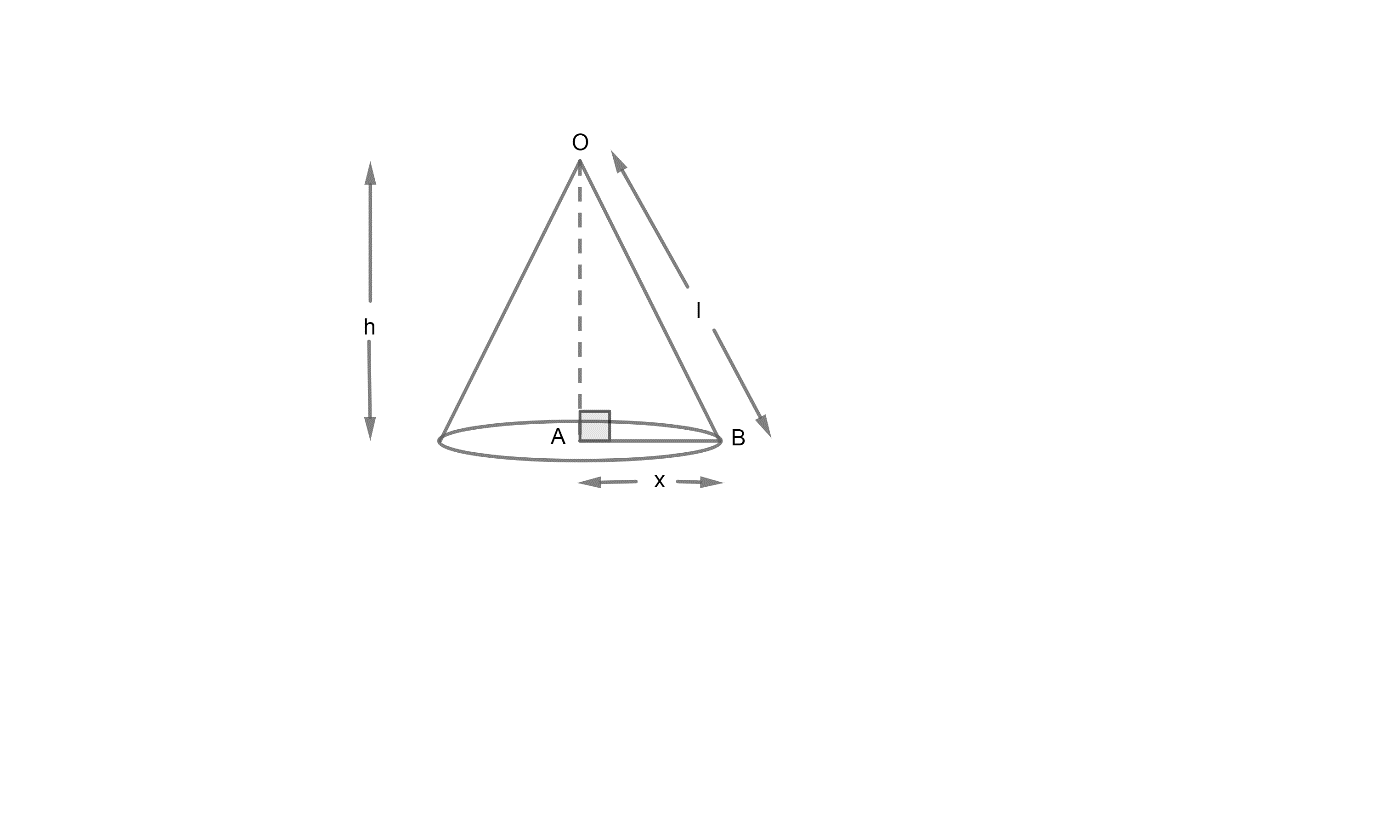
Now, we have in $\Delta OAB, \angle OAB=90{}^\circ $. Therefore, the triangle is a right angle triangle.
Now, we that according to the Pythagoras Theorem in a right angle triangle ABC as,

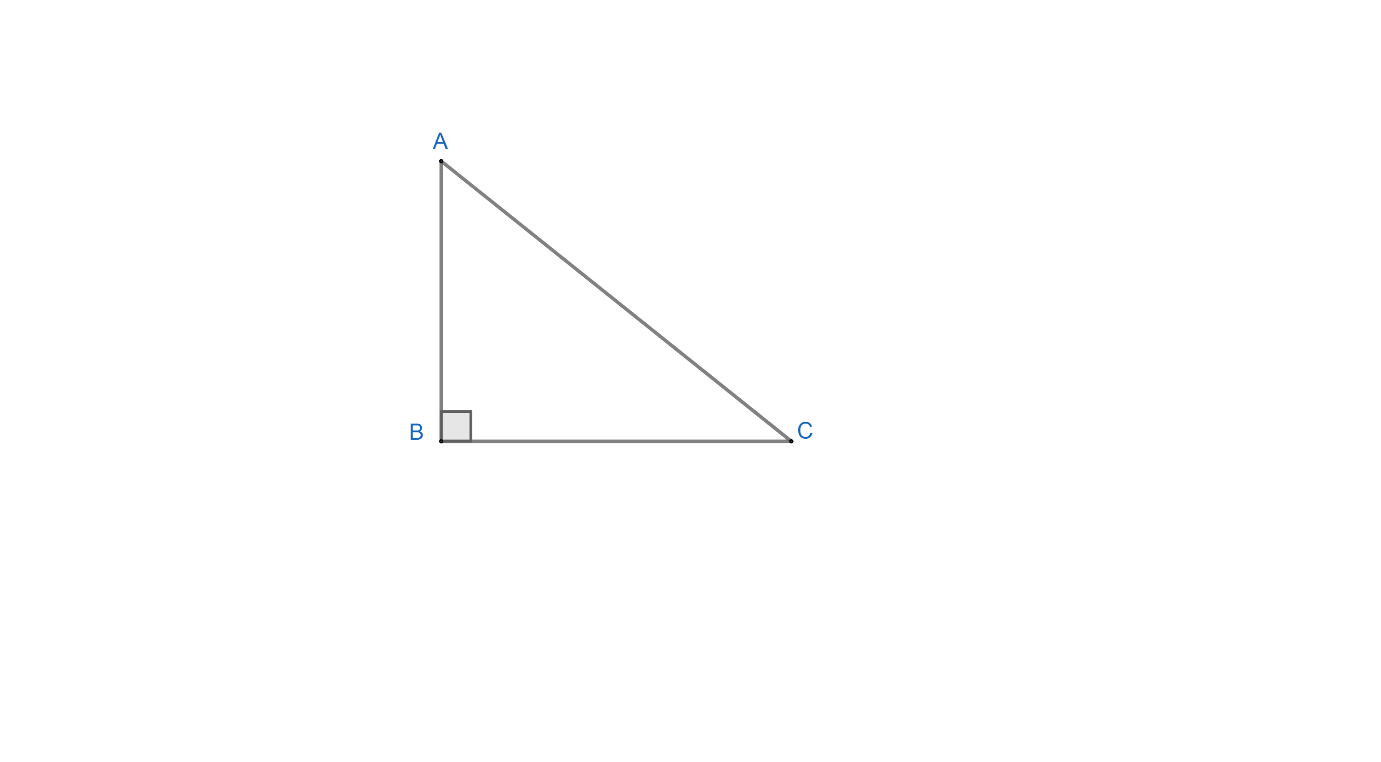
$A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$
Similarly, in $\Delta OAB$ we have,
$O{{B}^{2}}=O{{A}^{2}}+A{{B}^{2}}$
Now, we have $OB=l,\ OA=h,\ AB=radius$. So, using this we will find the value of radius as,
\[\begin{align}
  & {{l}^{2}}={{h}^{2}}+A{{B}^{2}} \\
 & A{{B}^{2}}={{l}^{2}}-{{h}^{2}} \\
 & AB=\pm \sqrt{{{l}^{2}}-{{h}^{2}}} \\
\end{align}\]
Now, since the radius of a cone is a positive quantity. Therefore, we have,
$\begin{align}
  & AB=\sqrt{{{l}^{2}}-{{h}^{2}}} \\
 & r=\sqrt{{{l}^{2}}-{{h}^{2}}} \\
\end{align}$
Hence, the correct option is (D).

Note: It is important to note that we have rejected $r=-\sqrt{{{l}^{2}}-{{h}^{2}}}$ because the radius of a cone cannot be negative, it has to be a positive quantity only. Therefore, we have rejected the negative value and accepted the positive value only.