
If $f\left( x \right) = \dfrac{x}{{{x^2} + 1}}$is increasing function then the value of x lies in the
$
{\text{A}}{\text{. }}R \\
{\text{B}}{\text{. }}\left( { - \infty ,1} \right) \\
{\text{C}}{\text{. }}\left( {1,\infty } \right) \\
{\text{D}}{\text{. }}\left( { - 1,1} \right) \\
$
Answer
588.6k+ views
Hint: Here we go through the properties of increasing and decreasing function as we know that when a function is increasing in nature then its first derivative is greater than zero.
Complete step-by-step answer:
Here in the question it is given that
$f\left( x \right) = \dfrac{x}{{{x^2} + 1}}$Is an increasing function
We know that if a function is increasing in nature that means its first derivative should be greater than zero.
i.e. $f'\left( x \right) > 0$
Now for solving the question we have to find out the first derivative of the given function.
Here the function is in the form of fraction so we apply the divisibility rule of derivative that we learn in differentiation chapter.
$
\Rightarrow f'\left( x \right) = \dfrac{{\dfrac{{d(x)}}{{dx}}\left( {{x^2} + 1} \right) - \dfrac{{d\left( {{x^2} + 1} \right)}}{{dx}}(x)}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\
\Rightarrow f'\left( x \right) = \dfrac{{\left( {{x^2} + 1} \right)(1) - x\left( {2x} \right)}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\
\Rightarrow f'\left( x \right) = \dfrac{{{x^2} + 1 - 2{x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\
\Rightarrow f'\left( x \right) = \dfrac{{1 - {x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\
$
Now given that f(x) is increasing function.
It means $f'\left( x \right) > 0$
i.e. $\dfrac{{1 - {x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}} > 0$
Now we can clearly see that ${\left( {{x^2} + 1} \right)^2}$ is always positive because of its square.
Or ${\left( {{x^2} + 1} \right)^2} > 0$
So for $f'\left( x \right) > 0$ we have to say $1 - {x^2} > 0$ ($\because $denominator is always positive and to make whole term positive numerator must be positive)
i.e. $\left( {1 - x} \right)\left( {1 + x} \right) > 0$
Now we represent it on number line we get,
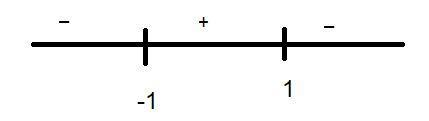
$ \Rightarrow - 1 < x < 1$
Or x lies in (-1, 1).
So, the correct answer is “Option D”.
Note: Whenever we face such a type of question the key concept for solving the question is always try to find out the derivative of the function when it is the question about the nature of the function either it is increasing or decreasing as we know that whenever a function is increasing then its derivative must be positive.
Complete step-by-step answer:
Here in the question it is given that
$f\left( x \right) = \dfrac{x}{{{x^2} + 1}}$Is an increasing function
We know that if a function is increasing in nature that means its first derivative should be greater than zero.
i.e. $f'\left( x \right) > 0$
Now for solving the question we have to find out the first derivative of the given function.
Here the function is in the form of fraction so we apply the divisibility rule of derivative that we learn in differentiation chapter.
$
\Rightarrow f'\left( x \right) = \dfrac{{\dfrac{{d(x)}}{{dx}}\left( {{x^2} + 1} \right) - \dfrac{{d\left( {{x^2} + 1} \right)}}{{dx}}(x)}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\
\Rightarrow f'\left( x \right) = \dfrac{{\left( {{x^2} + 1} \right)(1) - x\left( {2x} \right)}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\
\Rightarrow f'\left( x \right) = \dfrac{{{x^2} + 1 - 2{x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\
\Rightarrow f'\left( x \right) = \dfrac{{1 - {x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}} \\
$
Now given that f(x) is increasing function.
It means $f'\left( x \right) > 0$
i.e. $\dfrac{{1 - {x^2}}}{{{{\left( {{x^2} + 1} \right)}^2}}} > 0$
Now we can clearly see that ${\left( {{x^2} + 1} \right)^2}$ is always positive because of its square.
Or ${\left( {{x^2} + 1} \right)^2} > 0$
So for $f'\left( x \right) > 0$ we have to say $1 - {x^2} > 0$ ($\because $denominator is always positive and to make whole term positive numerator must be positive)
i.e. $\left( {1 - x} \right)\left( {1 + x} \right) > 0$
Now we represent it on number line we get,
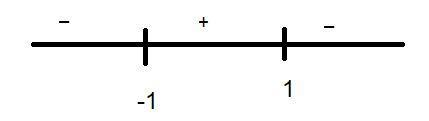
$ \Rightarrow - 1 < x < 1$
Or x lies in (-1, 1).
So, the correct answer is “Option D”.
Note: Whenever we face such a type of question the key concept for solving the question is always try to find out the derivative of the function when it is the question about the nature of the function either it is increasing or decreasing as we know that whenever a function is increasing then its derivative must be positive.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Name the part of the brain responsible for the precision class 11 biology CBSE

The growth of tendril in pea plants is due to AEffect class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




