Question

If $ f\left( x \right) = \dfrac{1}{{1 - x}},x \ne 0,1 $ , then the graph of the function $ y = f\left\{ {f\left( {f\left( x \right)} \right)} \right\},x > 1 $ is ?
(A) a circle
(B) an ellipse
(C) a straight line
(D) a pair of straight line

Answer 1

Hint: In the given question, we are required to find the nature of the graph of a composite function. We are given a function in the problem itself and we have to first calculate a composite function using the original function and then find out what the graph of the composite function represents. This question requires us to have the knowledge of basic and simple algebraic rules and operations such as substitution, addition, multiplication, subtraction and many more like these. A thorough understanding of functions, conic sections, coordinate geometry and its applications can be of great significance.

Complete step-by-step answer:
In the given question, we are given a function $ f\left( x \right) = \dfrac{1}{{1 - x}},x \ne 0,1 $ .
Now, we have to find a composite function using the given original function.
The composite function to be calculated is $ y = f\left\{ {f\left( {f\left( x \right)} \right)} \right\} $ .
So, we have to change the value of variable in the original function in order to find the composite function.
Now, we know that $ f\left( x \right) = \dfrac{1}{{1 - x}} $ .
So, to evaluate the composite function $ y = f\left\{ {f\left( {f\left( x \right)} \right)} \right\} $ , we substitute the value of $ f\left( x \right) $ as $ \dfrac{1}{{1 - x}} $ . Hence, we get,
 $ \Rightarrow y = f\left\{ {f\left( {\dfrac{1}{{1 - x}}} \right)} \right\} $
Now, to carry on the method of evaluating the composite function, we have to change the variable in the function $ f\left( x \right) = \dfrac{1}{{1 - x}} $ from x to $ \dfrac{1}{{1 - x}} $ .
So, we get,
 $ \Rightarrow y = f\left\{ {\dfrac{1}{{1 - \dfrac{1}{{1 - x}}}}} \right\} $
Taking the LCM and simplifying the expression, we get,
 $ \Rightarrow y = f\left\{ {\dfrac{1}{{\dfrac{{1 - x - 1}}{{1 - x}}}}} \right\} $
Cancelling the like terms with opposite signs, we get,
 $ \Rightarrow y = f\left\{ {\dfrac{{x - 1}}{x}} \right\} $
Now, we have to change the variable in the function $ f\left( x \right) = \dfrac{1}{{1 - x}} $ from x to $ \dfrac{{x - 1}}{x} $ . So, we get,
 $ \Rightarrow y = \left( {\dfrac{1}{{1 - \left( {\dfrac{{x - 1}}{x}} \right)}}} \right) $
Simplifying the expression further, we get,
 $ \Rightarrow y = \left( {\dfrac{1}{{\dfrac{{x - x + 1}}{x}}}} \right) $
Cancelling the like terms with opposite signs, we get,
 $ \Rightarrow y = x $
So, the composite function $ y = f\left\{ {f\left( {f\left( x \right)} \right)} \right\},x > 1 $ is equivalent to $ y = x $ .
Now, we know that the equation $ y = x $ actually represents a straight line on the Cartesian plane as the equation is a linear equation in two variables.
The graph of the composite function $ y = f\left\{ {f\left( {f\left( x \right)} \right)} \right\} $ can thus be plotted easily as $ y = x $ .
If $ x = 2 $ , $ y = x = 2 $ .
If $ x = 3 $ , $ y = x = 3 $ .
If $ x = 4 $ , $ y = x = 4 $ .
So, the graph of the function $ y = f\left\{ {f\left( {f\left( x \right)} \right)} \right\},x > 1 $ is as below:

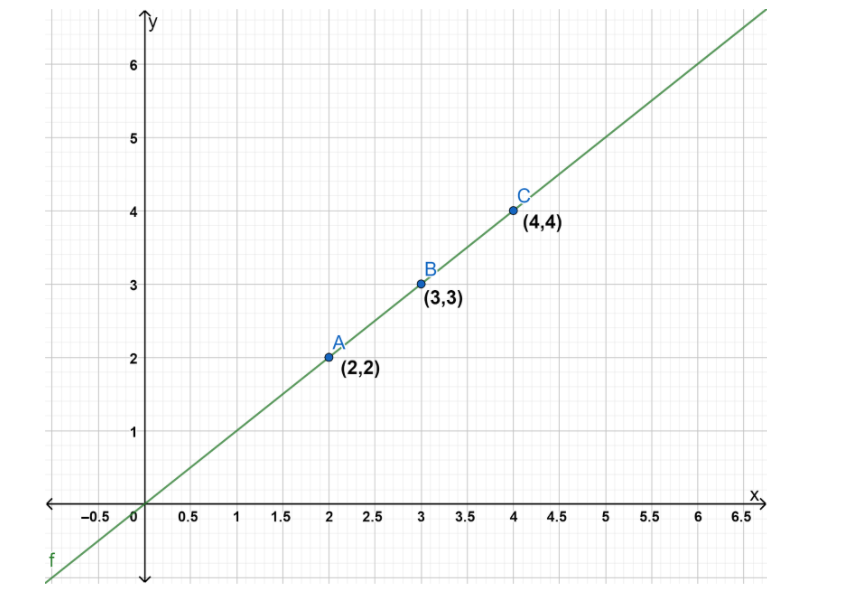
So, the graph of the function $ y = f\left\{ {f\left( {f\left( x \right)} \right)} \right\},x > 1 $ represents a straight line.
Hence, option (C) is correct.

Note: Such questions that require just simple change of variable can be solved easily by keeping in mind the algebraic rules such as substitution and transposition. Substitution of a variable involves putting a certain value in place of the variable. That specified value may be a certain number or even any other variable.