Question

If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

Answer 1

Hint- Here, we will proceed by using the property of the circle i.e., angle in the semicircle is always equal to ${90^0}$. Here, in order to prove that the given quadrilateral is a rectangle we will prove that all the interior angles of any rectangle is always equal to ${90^0}$.

Complete step by step answer:

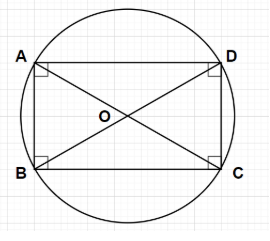
To prove: ABCD is a rectangle
Let us suppose ABCD be a cyclic quadrilateral with diagonals AC and BD as shown in the figure. Let 0 be the point where both the diagonals AC and BD intersect each other. Point O is also the centre of the circle.
Given, these diagonals AC and BD are diameters of the circle formed through the vertices A, B, C and D of the quadrilateral as shown in the figure.
According to the property of the circle, the angle subtended by the two lines drawn from the endpoints of the diameter of the circle at the circumference of the circle is always ${90^0}$ or the angle in the semicircle is always ${90^0}$.
Using the above property, we can write
$\angle {\text{ABC}} = {90^0},\angle {\text{BCD}} = {90^0},\angle {\text{CDA}} = {90^0}$ and $\angle {\text{DAB}} = {90^0}$.
i.e., all the interior angles of the quadrilateral ABCD is equal to ${90^0}$
According to the property of the rectangle, all the interior angles of any rectangle should always be equal to ${90^0}$
Hence, the quadrilateral ABCD is a rectangle.

Note- In this particular problem, the angle in the semicircle ABCO is $\angle {\text{ABC}}$ that’s why $\angle {\text{ABC}} = {90^0}$, the angle in the semicircle BCDO is $\angle {\text{BCD}}$ that’s why $\angle {\text{BCD}} = {90^0}$, the angle in the semicircle CDAO is $\angle {\text{CDA}}$ that’s why $\angle {\text{CDA}} = {90^0}$ and the angle in the semicircle DABO is $\angle {\text{DAB}}$ that’s why $\angle {\text{DAB}} = {90^0}$.