Question

If \[DE\;\parallel \;BC\]and \[AD = 1.7cm\], \[AB = 6.8cm\;\] and $AC=9cm$. Then length of AE is
A) 2.25 cm
B)4.5 cm
C)3.4 cm
D)5.1 cm

Answer 1

Hint: Here first we have to prove that by using the properties of similar triangles \[\Delta ADE \sim\Delta ABC\]and then we will compare the ratio of the corresponding sides of both the triangles to get the answer.
When two lines are parallel, then alternate exterior angles are equal.

Complete step by step solution:

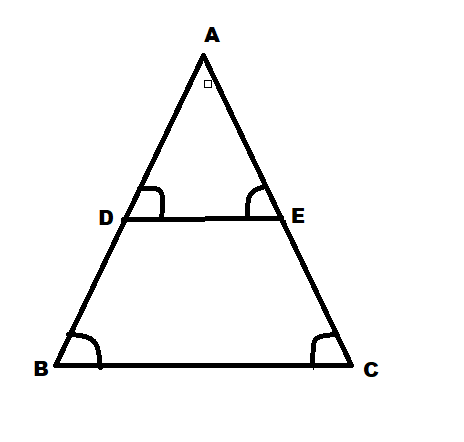
In \[\Delta ADE\] and \[\Delta ABC\]
\[\angle ABC = \angle ADE\] (alternate exterior angles)
\[\angle ACB = \angle AED\] (alternate exterior angles)
\[\angle A = \angle A\](common)
Therefore, \[\Delta ADE \sim \Delta ABC\] by AAA criterion.
Hence now we will compare the length of corresponding sides of both the triangles we get:
 \[\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}..............\left( 1 \right)\]
Since it is given that:
\[
 AD = 1.7cm \\
 AB = 6.8cm \\
 AC = 9cm \\
 \]
Therefore putting the respective values in equation 1 we get:
\[
\Rightarrow \dfrac{{1.7}}{{6.8}} = \dfrac{{AE}}{9} \\
\Rightarrow \dfrac{{AE}}{9} = \dfrac{1}{4} \\
\Rightarrow AE = \dfrac{9}{4}cm \\
 \Rightarrow AE = 2.25cm \\
 \]
Hence we get the length of AE= 2.25cm. Therefore option A is the correct option.

Note:
The similarity of triangles has several criteria:
AAA (angle-angle-angle) criterion in which the angles of the similar triangles are equal
SAS(side angle side) criterion in which two sides of similar triangles are in the same ratio and the angle between them is equal.
ASA(angle side angle) criterion in which two angles of the similar triangles are equal and the angle between them is equal.
SSS(side side side) criterion in which the ratio of the sides of the similar triangles are equal.