Question

If corresponding sides of two similar triangles are in the ratio of 4:9, then areas of these triangle are in the ratio of:
(a) 2:3
(b) 4:9
(c) 81:16
(d) 16:81

Answer 1

Hint: Consider two similar triangles $\Delta AMT\text{ and }\Delta AHE$ . Now use the property that the area of a triangle is half of the product of the length of two sides of the triangle with the sine of the angle between these two sides.

Complete step-by-step answer:
To start with the question, let us consider two similar triangles $\Delta AMT\text{ and }\Delta AHE$ .

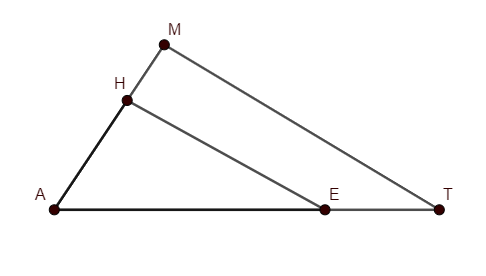
It is assumed that $\Delta AMT\sim \Delta AHE$ , and we know, two triangles are similar if their corresponding angles are equal and the corresponding sides are in proportion.
$\therefore \dfrac{MA}{HA}=\dfrac{AT}{AE}=\dfrac{TM}{EH}=\dfrac{4}{9}............(i)$
Also, $\angle AMT=\angle AHE.............(ii)$ .
Now we know that the area of a triangle is half of the product of the length of two sides of the triangle with the sine of the angle between these two sides.
$\therefore ar\left( \Delta AMT \right)=\dfrac{1}{2}\times MA\times TM\times \sin \left( \angle AMT \right)$
$\therefore ar\left( \Delta AHE \right)=\dfrac{1}{2}\times HA\times EH\times \sin \left( \angle AHE \right)$
Now we will find the ratio of the areas of the two triangles.
$\therefore \dfrac{ar\left( \Delta AMT \right)}{ar\left( \Delta AHE \right)}=\dfrac{\dfrac{1}{2}\times MA\times TM\times \sin \left( \angle AMT \right)}{\dfrac{1}{2}\times HA\times EH\times \sin \left( \angle AHE \right)}=\dfrac{MA}{HA}\times \dfrac{TM}{EH}\times \dfrac{\sin \left( \angle AMT \right)}{\sin \left( \angle AHE \right)}$
Now if we substitute the values of $\dfrac{MA}{HA}\text{ and }\dfrac{TM}{EH}$ from equation (i), we get
$\therefore \dfrac{ar\left( \Delta AMT \right)}{ar\left( \Delta AHE \right)}=\dfrac{4}{9}\times \dfrac{4}{9}\times \dfrac{\sin \left( \angle AMT \right)}{\sin \left( \angle AHE \right)}$
Also, from equation (ii), we know $\angle AMT=\angle AHE$ , so their sine would also be the same.
$\therefore \dfrac{ar\left( \Delta AMT \right)}{ar\left( \Delta AHE \right)}=\dfrac{4}{9}\times \dfrac{4}{9}=\dfrac{16}{81}$
Therefore, the answer to the above question is option (d).

Note: While using the relation of similarity, generally the students mix up the sides while it is clearly mentioned that the relation is valid only for the corresponding sides of similar triangles. If you want, you can solve the question using the heron’s formula of area of a triangle as well, but that would be a bit lengthier.