Question

If an equilateral triangle is inscribed in the circle \[{{x}^{2}}+{{y}^{2}}-6x-4y+5=0\] then the length of its side is
\[\left( a \right)\sqrt{6}\]
\[\left( b \right)2\sqrt{6}\]
\[\left( c \right)3\sqrt{6}\]
\[\left( d \right)4\sqrt{6}\]

Answer 1

Hint: To solve this question, compare the given equation of the circle to \[{{\left( x-p \right)}^{2}}+{{\left( y-q \right)}^{2}}={{r}^{2}}\] to get the radius r of the circle and centre (p, q) of the circle. To calculate \[{{\left( x-p \right)}^{2}}\] and \[{{\left( y-q \right)}^{2}}\] use the formula \[{{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab.\] Finally after calculating the radius, use the circle theorem, the angle subtended by an arc on the centre of the circle is twice at the circumference to get the length of the triangle.

Complete step by step answer:
Given that the equation of the circle is
\[{{x}^{2}}+{{y}^{2}}-6x-4y+5=0......\left( i \right)\]
We know that the standard equation of the circle with the centre at (p, q) and the radius r is given by
\[{{\left( x-p \right)}^{2}}+{{\left( y-q \right)}^{2}}={{r}^{2}}.....\left( ii \right)\]
Using equation (i) and equation (ii), we will try to calculate the radius r of the given circle. Consider equation (i).
\[{{x}^{2}}+{{y}^{2}}-6x-4y+5=0\]
By adding and subtracting 4 and 9, we will get
\[\Rightarrow {{x}^{2}}-6x+9-9+{{y}^{2}}-4y+4-4+5=0\]
\[\Rightarrow \left( {{x}^{2}}-6x+9 \right)+\left( {{y}^{2}}-4y+4 \right)-9-4+5=0\]
Using the formula, \[{{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\] in the above term \[\left( {{x}^{2}}-6x+9 \right)\] and \[\left( {{y}^{2}}-4y+4 \right),\] we get,
\[\text{Equation of circle}=\left( {{x}^{2}}-6x+9 \right)+\left( {{y}^{2}}-4y+4 \right)-8=0\]
\[\Rightarrow \text{Equation of circle}={{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=8\]
Comparing this from equation (ii), we get,
\[{{r}^{2}}=8\]
\[\Rightarrow r=\sqrt{8}\]
\[\Rightarrow r=2\sqrt{2}\]
Therefore, the radius of the circle is \[2\sqrt{2}\] and the centre of the circle is (p, q) = (3, 2). So, the situation is as below.

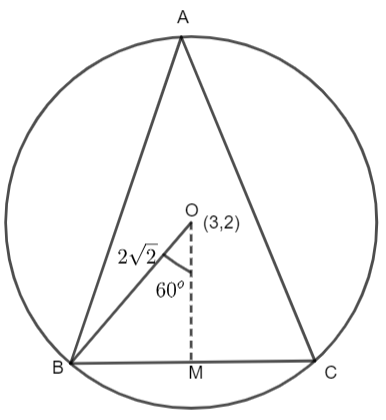
ABC is an equilateral triangle inscribed under the circle of radius \[2\sqrt{2}\] and centre (3, 2) = 0. Let us take the equilateral triangle to be of side a. We will drop a perpendicular on BC from O and name it as M. Now, because every angle of an equilateral triangle measure 60 degrees, we have,
\[\angle BAC={{60}^{\circ }}\]
Now, we have a theorem of the circle stated as “Angle subtended by an arc on the circle centre is double the angle subtended by the same arc on the circumference of the circle. Therefore, using this theorem, we have,
\[\angle BOC=2\times \angle BAC\]
\[\Rightarrow \angle BOC=2\times {{60}^{\circ }}\]
\[\Rightarrow \angle BOC={{120}^{\circ }}\]
Now, because OM is perpendicular to BC, so angle BOC is bisected into two equal angles BOM and MOC.
\[\Rightarrow \angle BOM=\dfrac{1}{2}\angle BOC\]
\[\Rightarrow \angle BOM=\dfrac{1}{2}\times {{120}^{\circ }}\]
\[\Rightarrow \angle BOM={{60}^{\circ }}\]
Now, consider triangle BOM.
\[\sin \angle BOM=\sin {{60}^{\circ }}=\dfrac{\text{perpendicular BM}}{\text{hypotenuse OB}}\]
As, \[OB=\text{radius r of the circle}=2\sqrt{2}\] , we have
\[\Rightarrow \sin {{60}^{\circ }}=\dfrac{BM}{2\sqrt{2}}\]
We know that \[\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}\] , so we can write that
\[BM=\dfrac{\sqrt{3}}{2}\times 2\sqrt{2}\]
\[\Rightarrow BM=\sqrt{6}\]
Then the length of BC is
\[BC=2BM\]
\[\Rightarrow BC=2\sqrt{6}\]
So, the side of the equilateral triangle ABC is \[2\sqrt{6}.\]

So, the correct answer is “Option B”.

Note: Another method to find the radius of the circle is given by if the equation of the circle is \[a{{x}^{2}}+2bxy+b{{y}^{2}}+2gx+2fy+c=0\] then the radius of the circle \[=\sqrt{{{g}^{2}}+{{f}^{2}}-c}.\] Here we had \[{{x}^{2}}+{{y}^{2}}-6x-4y+5=0.\]
\[\Rightarrow a=1;b=1;h=0;2g=-6\]
\[\Rightarrow g=-3\]
\[2f=-4;c=5\]
\[\Rightarrow f=-2\]
Then the radius is given by \[\sqrt{9+4-5}=\sqrt{8}=2\sqrt{2}.\] So, the radius of the unit is \[2\sqrt{2}\] units.