Question

If an angle is eight times its complementary angle, then the measurement of the angle is -
A. ${{90}^{\circ }}$\[\]
B. ${{20}^{\circ }}$\[\]
C. ${{80}^{\circ }}$\[\]
D. ${{160}^{\circ }}$ \[\]

Answer 1

Hint: Use the formula for the sum of two complementary angles to express both the angles in terms of an unknown variable. Then use the information given in the question to find out the measurement of the larger angle. Then verify further with the calculation for a smaller angle.\[\]

Complete step-by-step solution:

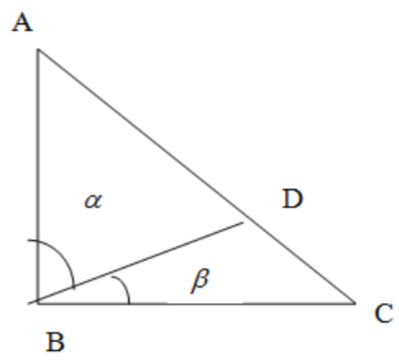
Two angles are called complementary when their sum of measurement is ${{90}^{\circ }}$. In the figure we can observe that the angles $\angle ABD$ and $\angle CBD$ are complimentary angles. Let us denote the measure of two said angles as $\alpha $ and $\beta $ respectively. From the definition of complimentary angles we get ,
\[\begin{align}
  & \alpha +\beta ={{90}^{\circ }} \\
 & \Rightarrow \beta ={{90}^{\circ }}-\alpha \\
\end{align}\]
So the required measure of two angles is expressed in terms of $\alpha $ as $\alpha $ and ${{90}^{\circ }}-\alpha $. \[\]
The question also states that the larger angle is eight times the smaller angle. In symbols we express as,
\[\begin{align}
  & \alpha =8\left( {{90}^{\circ }}-\alpha \right) \\
 & \Rightarrow \alpha ={{720}^{\circ }}-8\alpha \\
 & \Rightarrow 9\alpha ={{720}^{\circ }} \\
 & \Rightarrow \alpha ={{80}^{\circ }} \\
\end{align}\]
Hence the measurement of the asked angle is $ {{80}^{\circ }}$. We can also verify that the smaller will be one-eighth of ${{80}^{\circ }}$ which is equal to ${{90}^{\circ }}-{{80}^{\circ }}={{10}^{\circ }}$.
So the correct choice from the given options is C.

Note: The question tests your knowledge of complementary angles. We need the care of the confusion between complementary angles and supplementary angles. While in the case of complementary angles the sum of measurement is ${{90}^{\circ }}$, in the case of supplementary angles the sum of measurement is $ {{180}^{\circ }}$.