Question

If \[\alpha \] and \[\beta \] are the root of the equations \[\left( 2\sin x-\cos x \right)\left( 1+\cos x \right)=\sin x\] and \[3{{\sin }^{2}}x-10\cos x+3=0\], respectively and \[\alpha ,\beta \in \left[ 0,\dfrac{\pi }{2} \right]\]. So, find the value of \[\sin \left( \alpha -\beta \right)\].
a) 1
b) 0
c) $\dfrac{1-2\sqrt{6}}{6}$
d) $\dfrac{\sqrt{3}-2\sqrt{2}}{6}$

Answer 1

Hint: Solve both the equations to get the values of $\sin \alpha ,\cos \alpha ,\sin \beta $ and $\cos \beta $. Use the condition that $\alpha ,\beta $ will lie in 0 to $\dfrac{\pi }{2}$ only. Identity of $\sin \left( \alpha -\beta \right)$ can be given as

\[\sin \left( \alpha -\beta \right)=\sin \alpha \cos \beta -\cos \alpha \sin \beta \]

Put the evaluated values of $\sin \alpha ,\cos \alpha ,\sin \beta $ and $\cos \beta $ to the above equation to get value of \[\sin \left( \alpha -\beta \right)\].

Complete step-by-step answer:

So, \[\alpha \] is the root of the equation

\[\left( 2\sin x-\cos x \right)\left( 1+\sin x \right)={{\sin }^{2}}x\] ….......................................(i)

So, let us simplify the above equation.

So, we can multiply the brackets of equation (i) on the L.H.S side. So, we get

\[\left( 2\sin x-\cos x \right)\left( 1+\cos x \right)={{\sin }^{2}}x\]

\[2\sin x+2\sin x\cos x-\cos x-{{\cos }^{2}}x={{\sin }^{2}}x\]

\[2\sin x+2\sin x\cos x-\cos x-{{\cos }^{2}}x-{{\sin }^{2}}x=0\]

$2\sin x+2\sin x\cos x-\cos x-\left( {{\cos }^{2}}x+{{\sin }^{2}}x \right)=0$

We know the value of ${{\sin }^{2}}x+{{\cos }^{2}}x=1$ . So, we get the above expression as
$2\sin x+2\sin x\cos x-\cos x-1=0$

Now, taking $2\sin x$ as common from the first two terms of the above equation and ‘ $-1$ ’ from the last two terms. So, we get

$2\sin x+\left( 1+\cos x \right)-1\left( \cos x+1 \right)=0$

$\Rightarrow 2\sin x+\left( 1+\cos x \right)-1\left( 1+\cos x \right)=0$

$\left( 2\sin x-1 \right)\left( 1+\cos x \right)=0$

Now, we know multiplication of two numbers can be equals to 0, if either of them is 0.
So, we get

$2\sin x-1=0$ and $1+\cos x=0$

$\sin x=\dfrac{1}{2}$ and $\cos x=-1$

Now, as we know root of the given equation is $\alpha $ , so, we cannot take $\cos x=-1$ , as $\alpha $ is lying in $\left[ 0,\dfrac{\pi }{2} \right]$, where value of all the trigonometric functions is positive. Hence, $\cos x=-1$ can be ignored. So, we get

$\sin x=\dfrac{1}{2}$ ……………………………….(ii)

Now, we know the relation between $\sin \alpha $ and $\cos \alpha $ is given as

${{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1$

So, put $\sin \alpha =\dfrac{1}{2}$ to the above equation; so, we get

${{\left( \dfrac{1}{2} \right)}^{2}}+{{\cos }^{2}}\alpha =1$

${{\cos }^{2}}\alpha =1-\dfrac{1}{4}=\dfrac{3}{4}$

$\cos \alpha =\dfrac{\sqrt{3}}{2}$ , $\cos \alpha \ne \dfrac{-\sqrt{3}}{2}$

$\cos \alpha \ne \dfrac{-\sqrt{3}}{2}$, as $\alpha $ is lying in $\left[ 0,\dfrac{\pi }{2} \right]$.
Hence, we get

$\sin \alpha =\dfrac{1}{2}$ , $\cos \alpha =\dfrac{\sqrt{3}}{2}$ ……………………………..(iii)

Now, we know $\beta $ is the root of the equation

$3{{\cos }^{2}}x-10\cos x+3=0$ ………………………………….(iv)

Now, split the middle term of the above equation to $-9$ and $-1$ , to factorize the equation. So, we get

$3{{\cos }^{2}}x-9\cos x-\cos x+3=0$

Take $3\cos x$ common from the first two terms and $-1$ from the last two terms. So, we get

$3\cos x\left( \cos x-3 \right)-1\left( \cos x-3 \right)=0$

$\left( 3\cos x-1 \right)\left( \cos x-3 \right)=0$

So, we get $3\cos x-1=0$ or $\cos x-3=0$

$\cos x=\dfrac{1}{3}$ or $\cos x=3$

$\cos x\ne 3$, as the range of cosine functions is $\left[ -1,1 \right]$. So, ignore $\cos x=3$.

Now, we get the root of the equation (iv) is $\beta $. So, we get

$\cos \beta =\dfrac{1}{3}$

Now, we know


${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$

Hence, we can get the value of $\sin \beta $ using the above equation. So, we get

${{\sin }^{2}}\beta +{{\cos }^{2}}\beta =1$

${{\sin }^{2}}\beta +{{\left( \dfrac{1}{3} \right)}^{2}}=1$

${{\sin }^{2}}\beta =1-\dfrac{1}{9}=\dfrac{8}{9}$

$\sin \beta =\sqrt{\dfrac{8}{9}}=\dfrac{2\sqrt{2}}{3}$

Hence, we get

$\sin \beta =\dfrac{2\sqrt{2}}{3}$ , $\cos \beta =\dfrac{1}{3}$ ………………………………..(v)

Now, as we need to calculate the value of $\sin \left( \alpha -\beta \right)$. So, we know the

identity of $\sin \left( \alpha -\beta \right)$ as

\[\sin \left( \alpha -\beta \right)=\sin \alpha \cos \beta -\cos \alpha \sin \beta \]

 Now, use the equation (iii) and (v) to the above equation. So, we get

$\sin \left( \alpha -\beta \right)=\dfrac{1}{2}\times \dfrac{1}{3}-\dfrac{\sqrt{3}}{2}\times \dfrac{2\sqrt{2}}{3}$

$=\dfrac{1}{6}-\dfrac{2\sqrt{6}}{6}$

$\sin \left( \alpha -\beta \right)=\dfrac{1-2\sqrt{6}}{6}$

Hence, option (c) is the correct answer.

Note: Don’t take $\cos x=-1$ in the first equation, as $\alpha $ and $\beta $ are lying in $\left[ 0{}^\circ ,90{}^\circ \right]$ only, where $\left[ 0{}^\circ ,90{}^\circ \right]$ can never be negative. So, clear with this step and use all the information given in the problem.

One may use triangle approach as well to get $\cos \alpha $ using $\sin \alpha =\dfrac{1}{2}$ from first equation, and $\sin \beta $ by using $\cos \beta =\dfrac{1}{3}$ from the second equation. It can be done as

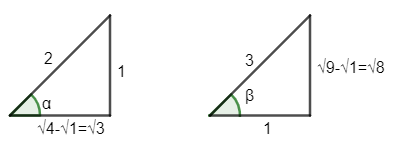
$\cos \alpha =\dfrac{\sqrt{3}}{2}$ , $\sin \beta =\dfrac{\sqrt{8}}{3}$