Question

If $a\in \mathbb{R}$and is not a multiple of $\pi $, then show that the function $f\left( x \right)=\cot x$ is differentiable at $a$ and $f\left( a \right)=-{{\operatorname{cosec}}^{2}}a.$. In general, $f'\left( x \right)=-{{\operatorname{cosec}}^{2}}x$ for all real $x\ne n\pi ,n\in \mathbb{Z}.$

Answer 1

Hint: To check the differentiability of any function, we may find the derivative of that function. To find the derivative of the function $f\left( x \right)$, we will use the first principle of derivative and the functional relation which is given in the question.

Complete step-by-step answer:
 In the question, we are given a function \[f\left( x \right)=\cot x\].
To test the differentiability of $f\left( x \right)$, we need to find the derivative of$f\left( x \right)$.
For this, we will use first principle from which we can find derivative $f'\left( x \right)$ of the function $f\left( x \right)$ by the formula,
$\Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{f\left( x+h \right)-f\left( x \right)}{h}$
In this question, we are given a function $f\left( x \right)=\cot x$ and $f\left( x+h \right)=\cot \left( x+h \right)$
\[\Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\cot \left( x+h \right)-\cot x}{h}..........\left( I \right)\]
In trigonometry, we have a formula, \[\cot \left( x+h \right)=\dfrac{\cot x\cot h-1}{\cot x+\cot h}\],
Substituting$\cot \left( x+h \right)$ from this formula in $\left( I \right)$, we get,
\[\begin{align}
  & f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\dfrac{\cot x\cot h-1}{\cot x+\cot h}-\cot x}{h} \\
 & \Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\cot x\cot h-1-\cot x\left( \cot x+\cot h \right)}{h\left( \cot x+\cot h \right)} \\
 & \Rightarrow f'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\dfrac{\cot x\cot h-1-{{\cot }^{2}}x-\cot x\cot h}{h\left( \cot x+\cot h \right)} \\
 & \Rightarrow f'\left( x \right)=(-1)\underset{h\to 0}{\mathop{\lim }}\,\dfrac{1+{{\cot }^{2}}x}{h\left( \cot x+\cot h \right)} \\
\end{align}\]
Since limit is with respect to $h$, we can take $1+{{\cot }^{2}}x$ out of the limit since $1+{{\cot }^{2}}x$ is a function of $x$.
$f'\left( x \right)=-\left( 1+{{\cot }^{2}}x \right)\underset{h\to 0}{\mathop{\lim }}\,\dfrac{1}{h\left( \cot x+\cot h \right)}$
$\Rightarrow f'\left( x \right)=-\left( 1+{{\cot }^{2}}x \right)\underset{h\to 0}{\mathop{\lim }}\,\dfrac{1}{h\cot x+h\cot h}.......\left( II \right)$
Solving limit part in $\left( II \right)$ i.e. $\underset{h\to 0}{\mathop{\lim }}\,\dfrac{1}{h\cot x+h\cot h}$,
The term $h\cot x=0$ for $h\to 0$ and the term $h\cot h=\dfrac{h}{\tan h}=1$ for $h\to 0$.
$\Rightarrow \underset{h\to 0}{\mathop{\lim }}\,\dfrac{1}{h\cot x+h\cot h}=1$
Substituting this value of limit in equation$\left( II \right)$, we get,
$f'\left( x \right)=-\left( 1+{{\cot }^{2}}x \right)$
Also, in trigonometry, we have a formula $1+{{\cot }^{2}}x={{\operatorname{cosec}}^{2}}x.$ So using this formula, we have,
$\Rightarrow f'\left( x \right)=-{{\operatorname{cosec}}^{2}}x.........(III)$
Drawing graph of $f'\left( x \right)$,

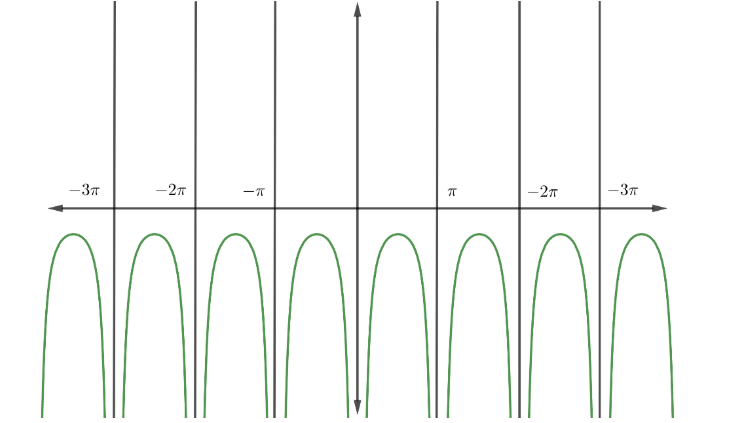
We can see that the graph of $f'\left( x \right)$ is discontinuous at multiples of $\pi $. So, \[\left\{ ......-3\pi ,-2\pi ,-\pi ,0,\pi ,2\pi ,3\pi ,..... \right\}\]
This means that $f\left( x \right)$ is differentiable for $x\in \mathbb{R}-\left\{ \text{multiple of }\pi \right\}$
Also from $\left( III \right)$, we have,
$\Rightarrow f'\left( x \right)=-{{\operatorname{cosec}}^{2}}x$
If we substitute $x=a$ in the above equation, we get,
$\Rightarrow f'\left( a \right)=-{{\operatorname{cosec}}^{2}}a$

Note: The question might have taken a lesser amount of time, if one had remembered the derivative of function $f\left( x \right)=\cot x$ instead of finding it using the first principle of derivative.