Question

If $AD$ and $PM$ are medians of triangles $ABC$ and $PQR$ , respectively where $\Delta ABC\sim \Delta PQR$. Then, prove that $\dfrac{AB}{PQ}=\dfrac{AD}{PM}$.

Answer 1

Hint: For solving this first we will use the property of the median and then use the side angle side criterion to prove the triangles similar so that we can prove the desired result.

Complete step-by-step answer:

Given:
It is given that, $\Delta ABC\sim \Delta PQR$ and $AD$ is the median of $\Delta ABC$ and $PM$ is the median of $\Delta PQR$ . The figure of these two triangles is given below:

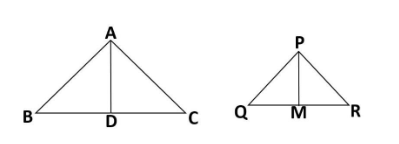
Now, in the above figure, as $AD$ and $PM$ both are medians, they will divide the opposite side of the triangles in two equal parts. Then,
$\begin{align}
  & BD=DC=\dfrac{BC}{2} \\
 & \Rightarrow 2BD=2DC=BC..........\left( 1 \right) \\
 & QM=MR=\dfrac{QR}{2} \\
 & \Rightarrow 2QM=2MR=QR..........\left( 2 \right) \\
\end{align}$
Now, it is given that $\Delta ABC\sim \Delta PQR$ . As we know that in any two similar triangles corresponding angles of the triangles are equal and the ratio of corresponding sides is also equal. Then,
$\begin{align}
  & \angle ABD=\angle PQM.........\left( 3 \right) \\
 & \dfrac{AB}{PQ}=\dfrac{BC}{QR} \\
\end{align}$
Now, substituting $BC=2BD$ from equation (1) and $QR=2QM$ from equation (2) in the above equation. Then,
$\begin{align}
  & \dfrac{AB}{PQ}=\dfrac{BC}{QR}=\dfrac{2BD}{2QM} \\
 & \Rightarrow \dfrac{AB}{PQ}=\dfrac{BD}{QM}............\left( 4 \right) \\
\end{align}$
Now, consider $\Delta ABD$ and $\Delta PQM$ . From equation (3) and equation (4) we have:
$\begin{align}
  & \angle ABD=\angle PQM \\
 & \dfrac{AB}{PQ}=\dfrac{BD}{QM} \\
\end{align}$
Thus, from the side angle side criterion as one angle of two triangles are equal and the ratio of the sides making that angle is also equal so, the triangles will be similar to each other. Then,
$\Delta ABD\sim \Delta PQM$
Now, as we know that in a similar triangle the ratio of corresponding sides is equal. Then,
$\dfrac{AB}{PQ}=\dfrac{AD}{PM}$
Thus, we have proved that $\dfrac{AB}{PQ}=\dfrac{AD}{PM}$ .
Hence, proved.

Note: Here, the student should correctly apply the properties of triangles and proceed stepwise to solve the question. Moreover, be careful in writing the name of similar triangles. For example in this question we cannot write that $\Delta ABD\sim \Delta PMQ$ , the correct way is $\Delta ABD\sim \Delta PQM$.