Question

If AD = 5.7 cm, BD = 9.5 cm, AE = 3.6 cm and EC = 6 cm, then DE || BC.
(a) Yes
(b) No
(c) Can’t say
(d) Ambiguous

Answer 1

Hint: AB and AC are intercepts on the lines BC and DE. If the intercepts are in the same ratio between the lines BC and DE, then by basic proportionality theorem, the lines BC and DE are parallel.

Complete step-by-step answer:
If a line is parallel to a side of a triangle that intersects the other sides of the triangle at two distinct points, then the line divides those sides of the triangle in proportion.
It is a basic result of the equal intercept theorem which states that if a transversal makes equal intercepts on three or more parallel lines then any other transversal cutting them will also make equal intercepts.
Now, we have triangle ABC, and the line DE intersects the sides AB and AC at D and E respectively.

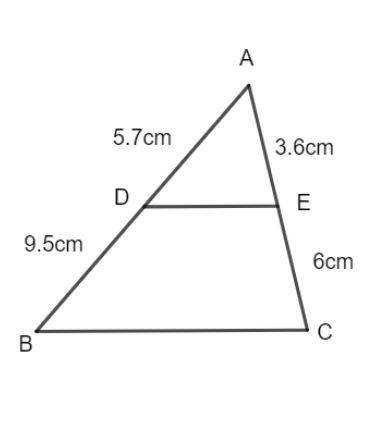
We now find the ratio of AD and BD as follows:
\[\dfrac{{AD}}{{BD}} = \dfrac{{5.7}}{{9.5}}\]
Simplifying the above expression, we have:
\[\dfrac{{AD}}{{BD}} = \dfrac{3}{5}..........(1)\]
We now find the ratio of AE and CE as follows:
\[\dfrac{{AE}}{{CE}} = \dfrac{{3.6}}{6}\]
Simplifying the above expression, we have:
\[\dfrac{{AE}}{{CE}} = \dfrac{3}{5}........(2)\]
From equation (1) and equation (2), we have:
\[\dfrac{{AE}}{{CE}} = \dfrac{{AD}}{{BD}}\]
Hence, the sides are divided into equal ratios.
Hence, by proportionality theorem, DE is parallel to BC.
Hence, the correct answer is option (a).

Note: It is very vague from the given question, so, draw the diagram first and then it becomes easy to solve and determine the correct answer.