Question

If ABCD is a quadrilateral, then $\overline{AC}=\overline{AD}-\_\_\_\_\_$ .
(a) $\overline{AD}$
(b) $\overline{BC}$
(c) $\overline{CD}$
(d) $\overline{AC}$

Answer 1

Hint: As ABCD is a quadrilateral and ACD is a triangle which is also a polygon, we can use the rule of vector addition of a polygon to solve the above question. According to the rule the sum of the vectors forming all the sides of the polygon such that the tail of one vector coincides with the head of the other vector is zero. Also, use the identity that $\overline{DA}=-\overline{AD}$ .

Complete step-by-step answer:
Let us start the solution to the above question by drawing a representative diagram of the situation given in the question.

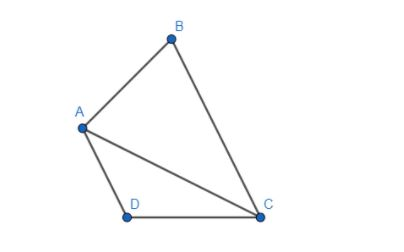
We know that according to the polygon law of vector addition the sum of the vectors forming all the sides of the polygon such that the tail of one vector coincides with the head of the other vector is zero. So, if we apply this on triangle ADC, we get
$\overline{DA}+\overline{CD}+\overline{AC}=0$
$\Rightarrow \overline{AC}=-\overline{DA}-\overline{CD}$
We also know that $\overline{DA}=-\overline{AD}$ .
\[\overline{AC}=\overline{AD}-\overline{CD}\]

So, the correct answer is “Option C”.

Note: You should know that polygon law is an extension of triangle law of vector addition and the above question could have been solved using triangle law as well. Also, remember that for applying the polygon law, the head of one vector must coincide with the tail of the other and directions of vectors are very important.