Question

If ABCD is a parallelogram with \[A(5,4),B(-1,-2),C(8,-2)\]. How do you find the coordinates of D?

Answer 1

Hint: We are given coordinates of three vertices of a parallelogram and we are asked to find out the coordinate of the fourth vertex. We will be using the properties of a parallelogram that the opposite sides of a parallelogram are parallel and are equal in length. So, we will use the distance formula, which is, \[\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\], where \[(x_{1},y_{1})\] and \[(x_{2}, y_{2})\] are coordinates of points, to find the coordinate of the fourth vertex.

Complete step by step solution:
According to the given question, we are given the coordinates of three vertices of a parallelogram and we have to find the coordinate of the fourth vertex.
Parallelogram can be said to be a quadrilateral which has the opposite sides equal and parallel. And the diagonals of a parallelogram bisect each other.
Based on the given coordinates, we have the following figure,

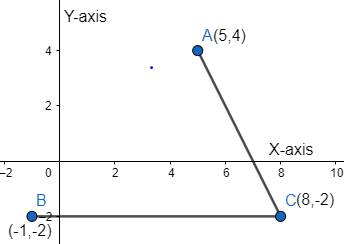
Let the coordinate of the fourth vertex be \[D(x,y)\].
So, we have,

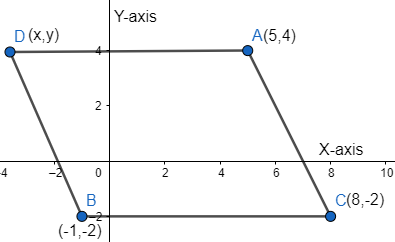
As we know that, the opposite sides of a parallelogram are equal, that means,
\[DA=BC\] and \[DB=AC\]
Now, we will use the distance formula for points with coordinates \[(x_{1},y_{1})\] and \[(x_{2}, y_{2})\] is given by \[\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\] and equate the distances and find the values of x and y.
Distance of DA = Distance of BC
\[\Rightarrow \sqrt{{{(5-x)}^{2}}+{{(4-y)}^{2}}}=\sqrt{{{(8-(-1))}^{2}}+{{(-2-(-2))}^{2}}}\]
Squaring both the sides, we get the expression as,
\[\Rightarrow {{(5-x)}^{2}}+{{(4-y)}^{2}}={{(8-(-1))}^{2}}+{{(-2-(-2))}^{2}}\]
Opening up the brackets, we have,
\[\Rightarrow 25-10x+{{x}^{2}}+16-8y+{{y}^{2}}={{(8+1)}^{2}}+{{(-2+2)}^{2}}\]
Solving further, we get the equation as,
\[\Rightarrow {{x}^{2}}-10x+{{y}^{2}}-8y+25+16={{(9)}^{2}}\]
\[\Rightarrow {{x}^{2}}-10x+{{y}^{2}}-8y+41=81\]
\[\Rightarrow {{x}^{2}}-10x+{{y}^{2}}-8y=40\]-----(1)

Then, distance of DB = distance of AC
\[\Rightarrow \sqrt{{{(-1-x)}^{2}}+{{(-2-y)}^{2}}}=\sqrt{{{(8-5)}^{2}}+{{(-2-4)}^{2}}}\]
Squaring both the sides, we get the expression as,
\[\Rightarrow {{(-1-x)}^{2}}+{{(-2-y)}^{2}}={{(8-5)}^{2}}+{{(-2-4)}^{2}}\]
Opening up the brackets, we have,
\[\Rightarrow 1+2x+{{x}^{2}}+4+4y+{{y}^{2}}={{3}^{2}}+{{(-6)}^{2}}\]
Solving further, we get the equation as,
\[\Rightarrow {{x}^{2}}+2x+1+{{y}^{2}}+4y+4=9+36\]
\[\Rightarrow {{x}^{2}}+2x+{{y}^{2}}+4y+5=45\]
\[\Rightarrow {{x}^{2}}+2x+{{y}^{2}}+4y=40\]-----(2)

Now, we will subtract the two equations, that is,
equation (1) – equation (2)
\[\Rightarrow ({{x}^{2}}-10x+{{y}^{2}}-8y)-({{x}^{2}}+2x+{{y}^{2}}+4y)=40-40\]
Opening up the brackets, we have,
\[\Rightarrow {{x}^{2}}-10x+{{y}^{2}}-8y-{{x}^{2}}-2x-{{y}^{2}}-4y=0\]
\[\Rightarrow -12x-12y=0\]
Reducing the equation, we get,
\[\Rightarrow x+y=0\]
\[\Rightarrow x=-y\]----(3)
Now, we will substitute the equation (3) in equation (2), we get,
\[\Rightarrow {{(-y)}^{2}}-10(-y)+{{y}^{2}}-8y=40\]
\[\Rightarrow {{y}^{2}}+10y+{{y}^{2}}-8y=40\]
Solving further, we get the expression as,
\[\Rightarrow 2{{y}^{2}}+2y-40=0\]
\[\Rightarrow {{y}^{2}}+y-20=0\]
Now, we will factorize the above expression as,
\[\Rightarrow {{y}^{2}}+5y-4y-20=0\]
\[\Rightarrow y(y+5)-4(y+5)=0\]
\[\Rightarrow (y+5)(y-4)=0\]
Equating the factors to zero, we get the value of \[y\] as,
\[\Rightarrow y=4,-5\]
Substituting the values of \[y\] in equation (3), we get,
When \[y=4\], then \[x=-y=-4\]
And when \[y=-5\], then
\[x=-y=-(-5)\]
\[\Rightarrow x=5\]
 the coordinates of D are
\[D=(-4,4)~~or~(5,-5)\]
That is, we have something as below,

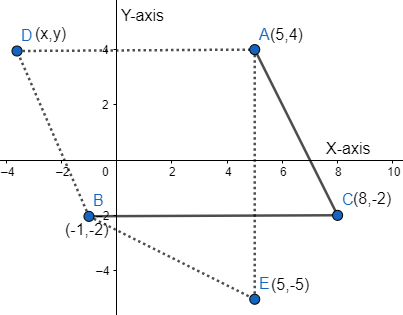
But as we know that, in a parallelogram, the opposite sides are equal and parallel. So, we will take the value of \[D=(-4,4)\]. So, we have the parallelogram as follows,

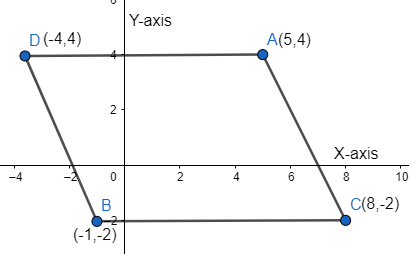
Therefore, the coordinate of \[D(-4,4)\].

Note: Properties of a parallelogram should be known only then the above question can be solved. When we solved for the coordinate, we got two values of \[D=(-4,4)~~or~(5,-5)\]. Since, taking \[(5,-5)\] will give us a quadrilateral whose sides are intersecting and not parallel and it is not a property of a parallelogram.