Question

If \[AB\] and \[CD\] are two chords of a circle which when produced to meet at a point \[P\] such that \[AB = 5{\rm{cm}}\], \[AP = 8{\rm{cm}}\] and \[CD = 2{\rm{cm}}\] then \[PD = \]
A.12 cm
B.5 cm
C.6 cm
D.cm

Answer 1

Hint: Here, we will first draw a figure using the given information. Then we will use the intersecting secant theorem to frame a quadratic equation. We will then solve the obtained equation by factorization method to the required length of \[PD\].

Complete step-by-step answer:
According to the question,
\[AB\]and \[CD\] are two chords of a circle
Also, they are produced to meet at a point \[P\].
It is given that \[AB = 5{\rm{cm}}\], \[AP = 8{\rm{cm}}\]and \[CD = 2{\rm{cm}}\]
And, we are required to find the length of \[PD\]

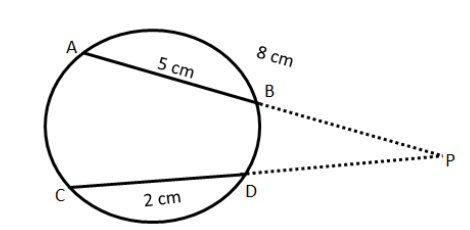
Now, by intersecting secant theorem, we know that,
\[PA \times PB = PC \times PD\]……………………………………\[\left( 1 \right)\]
Now from the figure we can see, \[PC = \left( {PD + CD} \right)\]
And, it is given that \[AP = 8{\rm{cm}}\]
Also, \[AB = 5{\rm{cm}}\] and \[AP = 8{\rm{cm}}\],
Therefore, \[PB = \left( {AP - AB} \right) = \left( {8 - 5} \right) = 3{\rm{cm}}\]
Hence, substituting these values in equation \[\left( 1 \right)\], we get,
\[8 \times 3 = \left( {PD + CD} \right) \times PD\]
According to the question, \[CD = 2{\rm{cm}}\], hence substituting this value,
\[ \Rightarrow 24 = \left( {PD + 2} \right) \times PD\]
Now, opening the brackets and solving further, we get,
\[ \Rightarrow P{D^2} + 2PD - 24 = 0\]
The above equation is a quadratic equation. We will factorize this equation to find the required value.
Splitting the middle term, we get
\[ \Rightarrow P{D^2} + 6PD - 4PD - 24 = 0\]
$\Rightarrow PD\left( PD+6 \right)-4\left( PD+6 \right)=0$
Taking the brackets common, we get
\[ \Rightarrow \left( {PD - 4} \right)\left( {PD + 6} \right) = 0\]
By zero product property, we get
\[ \Rightarrow \left( {PD - 4} \right) = 0\]
\[ \Rightarrow PD = 4{\rm{cm}}\]
Or
\[ \Rightarrow \left( {PD + 6} \right) = 0\]
\[ \Rightarrow PD = - 6{\rm{cm}}\]
But, length can’ be negative.
Therefore, rejecting the negative value, we get,
\[PD = 4{\rm{cm}}\]
Hence, option D is the correct answer.

Note: A chord of a circle is a straight line segment whose endpoints lie on the circumference of the circle. By intersecting secant theorem, we mean that if two secant segments are drawn to a circle from an external point then the product of one internal and external secant is equal to the product of the second internal and external secant. Here, secant is a straight line that cuts a circle at two or more parts.