Question

If A=${30^ \circ }$, a=7, b=8 in triangle ABC, then prove that B has two solutions.

Answer 1

Hint:-In order to solve this problem we need to use sine rule and solve. We know the formula that \[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}}\], where a, b are sides of triangles and A, B are angles of triangle opposite to side a and b.

Complete step by step answer:

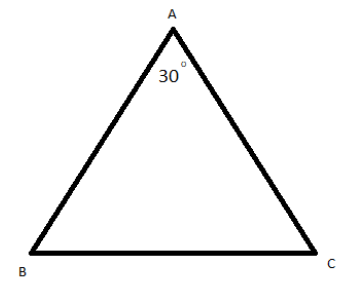
Above figure is the diagram of the triangle where AB = c, BC=a and AC = b.
As from sine rule,
\[\dfrac{{\text{a}}}{{{\text{sinA}}}}{\text{ = }}\dfrac{{\text{b}}}{{{\text{sinB}}}}\]

$ \Rightarrow {\text{sinB = }}\dfrac{{\text{b}}}{{\text{a}}}{\text{sinA = }}\dfrac{{\text{8}}}{{\text{7}}}{\text{ }\times }\dfrac{{\text{1}}}{{\text{2}}}{\text{ = }}\dfrac{{\text{4}}}{{\text{7}}}$
​ As B is between (0,π), we have two solution
$ \Rightarrow B = {\sin ^{ - 1}}\left( {\dfrac{4}{7}} \right)\,\,\,\,\,{\text{and }}\,\,\,\pi - {\sin ^{ - 1}}\left( {\dfrac{4}{7}} \right)$
Hence, the two solutions of B can be written as:
$B = {\sin ^{ - 1}}\left( {\dfrac{4}{7}} \right)\,\,\,\,{\text{and}}\,\,\,\pi - {\sin ^{ - 1}}\left( {\dfrac{4}{7}} \right)$

Note:- In this problem we have to use the sine rule that is \[\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}}\] and need to know about the quadrant in which quadrant what is the value of angle. Proceeding with this you will get the correct answer.