Question

If A(2, 0), B(0, 2), C(0, 7) and D(x, y) are the vertices of an isosceles trapezium in which AB is the parallel to DC, then D is
A. (7, 0) or (2, 5)
B. (2, 0) or (7, 5)
C. (0, 5) or (2, 7)
D. (0, 7) or (2, 5)

Answer 1

Hint: We had to form two equations and then solve them to get the required value of x and y. We will first equation by comparing the slope of parallel lines where formula of slope is \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]. And another equation by comparing the length of equal sides.

Complete step-by-step answer:

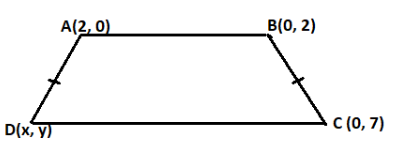
As we know that if two lines are parallel then their slope must be equal.
And the formula for finding the slope of line joining the points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] will be \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\].
Now as it is given in the question that the sides AB and DC are parallel to each other. So, the slopes of lines AB and DC should be equal.
So, comparing their slopes. We get,
\[
  \dfrac{{2 - 0}}{{0 - 2}} = \dfrac{{7 - y}}{{0 - x}} \\
   - 1 = \dfrac{{7 - y}}{{ - x}} \\
\]
Now cross multiplying both sides of the above equation. We get,
x = 7 – y $\to$ (1)
Now as it is given in the question the trapezium ABCD is an isosceles trapezium. And we know that the non-parallel sides of the isosceles trapezium are equal.
So, AD = BC
Now, we had to find the length of line AD and BC.
So, as we know that according to distance formula length of the line joining two points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] is calculated as \[\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \].
So, now applying the distance formula to find the length of AD and BC and then comparing them. We get,
\[\sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 0} \right)}^2}} = \sqrt {{{\left( {0 - 0} \right)}^2} + {{\left( {7 - 2} \right)}^2}} \]
Now square both sides of the above equation. We get,
\[{\left( {x - 2} \right)^2} + {\left( y \right)^2} = {\left( 5 \right)^2}\] $\to$ (2)
Now putting the value of x from equation 1 to equation 2. We get,
\[{\left( {7 - y - 2} \right)^2} + {\left( y \right)^2} = {\left( 5 \right)^2}\]
\[{\left( {5 - y} \right)^2} + {\left( y \right)^2} = {\left( 5 \right)^2}\] $\to$ (3)
As we know the identity that a and b are two number then \[{\left( {a - b} \right)^2} = {\left( a \right)^2} + {\left( b \right)^2} - 2ab\]
So, equation 3 becomes,
\[
  {\left( 5 \right)^2} + {\left( y \right)^2} - 10y + {\left( y \right)^2} = {\left( 5 \right)^2} \\
  2{\left( y \right)^2} - 10y = 0 \\
  2y\left( {y - 5} \right) = 0 \\
\]
So, y = 5 or y = 0.
Now putting the value of y in equation 1. We get,
When y = 5 then x = 7 – y = 7 – 5 = 2
When y = 0 then x = 7 – y = 7 – 0 = 7
So, the point D will be (2, 5) or (7, 0)
Hence, the correct option will be A.

Note: Whenever we come up with this type of problem we have to find the number of equations such that they are more than the number of variables. Like here there are two variables x and y. So, we had to form two equations, we will form the first equation by using the condition that the slope of parallel lines is equal. So, the slope of lines AB and DC must be equal and the formula for finding the slope of line joining the points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] will be \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\]. And after that we form second equation by finding the length of side AD and BC by using distance formula which states that the length of the line joining two points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] is calculated as \[\sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]. And they equate the length of sides AD and BC because ABCD is an isosceles trapezium and the non-parallel sides of the isosceles trapezium are equal. After that we had to solve these two equations to get the required value of x and y. And this will be the easiest and efficient way to find the solution of the problem.