Question

If a trigonometric expression is given as \[\sin \theta =\cos \theta \], then the value of \[\theta \] is:
(A). \[{{0}^{\circ }}\]
(B). \[{{45}^{\circ }}\]
(C). \[{{60}^{\circ }}\]
(D). \[{{30}^{\circ }}\]

Answer 1

Hint: At first consider a triangle ABC with a right angle and an angle \[\theta \]. Then define \[\sin \theta \] and \[\cos \theta \] according to sides and equalize them to prove that triangle is an isosceles right-angled triangle.

Complete step-by-step solution -
In the question we are given an equation \[\sin \theta =\cos \theta \] and we have to find value of \[\theta \] so that given equation satisfies.
Before proceeding we will learn about sine and cosine function.
In mathematics, the sine is a trigonometric function of an angle. The sine of an acute in the context of a right-angled triangle for the specified angle is the ratio of the length of the side that is opposite to that angle to the length of the longest side of the triangle.
Now let’s define the cosine function of an acute angle \[\theta \], at first start with a right-angle triangle that contains an angle of measure \[\theta \] in the accompanying figure, angle A in the \[\Delta ABC\] is the angle of interest.

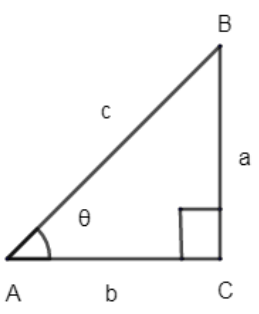
The three sides of the triangle are named as follows: -
The opposite side is the side opposite of the angel of interest as a.
       (ii) The hypotenuse is side opposite to the right angle as h.
       (iii) The adjacent side id the remaining side in this case side as b.
So, we represent \[\sin \left( \theta \right)\] = $\dfrac {\text{opposite side}}{\text{hypotenuse}}$
So here \[\sin \theta =\cos \theta \] is given which can also be represented as
 $\dfrac {\text{Opposite side}}{\text{Hypotenuse}}$ = $\dfrac {\text{Adjacent side}}{\text{Hypotenuse}}$
So, $\text{opposite side} = \text{Adjacent side}.$
Hence, we can say that the triangle ABC is an isosceles right-angled triangle as the two sides are the same and there is a right angle too.
So, the measure of \[\theta \] is \[{{45}^{\circ }}\].
Hence the correct option is (b).

Note: One can also do the same problem by another method. At first divide the whole given equation \[\sin \theta =\cos \theta \] by \[\cos \theta \] then we will get \[\tan \theta =1\] and we know that the value of \[\tan {{45}^{\circ }}\] is 1 so the value of \[\theta \] will be \[{{45}^{\circ }}\].