Question

If a triangle and a $\parallel gm$ are on the same base and between same parallel. Then find the ratio of their areas.

Answer 1

Hint:
We begin by drawing a corresponding figure. Then find the area of the parallelogram which is the product of the base and the perpendicular height between two parallel lines. Next, find the area of the triangle which is half the product of the base and the perpendicular height. At last, find the ratio by substituting the values in $\dfrac{{{\text{area}}\left( {\square {\text{ABCD}}} \right)}}{{{\text{area}}\left( {\vartriangle {\text{AEB}}} \right)}}$

Complete step by step solution:
We are given that the triangle and parallelogram are on the base and between the parallel lines.
First of all, let us draw the corresponding diagram,

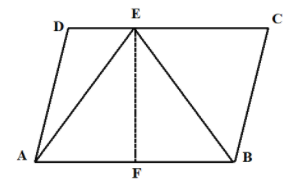
Here, ABCD is a parallelogram and AEB is a triangle on the base AB, where ${\text{AB}}\parallel {\text{CD}}$.
We know that area of the parallelogram is the product of the base and the perpendicular height between two parallel lines.
Then, the area of parallelogram is ${\text{AB}} \times {\text{FE}}$
Now, we know that the area of the triangle is half the product of the base and the perpendicular height.
That is the area of triangle AEB is $\dfrac{1}{2}\left( {{\text{AB}} \times {\text{FE}}} \right)$
Now, we have to find the ratio of their area.
That is we want to find $\dfrac{{{\text{area}}\left( {\square {\text{ABCD}}} \right)}}{{{\text{area}}\left( {\vartriangle {\text{AEB}}} \right)}}$
Substitute the values,
$\dfrac{{{\text{area}}\left( {\square {\text{ABCD}}} \right)}}{{{\text{area}}\left( {\vartriangle {\text{AEB}}} \right)}} = \dfrac{{{\text{AB}} \times {\text{FE}}}}{{\dfrac{1}{2}\left( {{\text{AB}} \times {\text{FE}}} \right)}} = \dfrac{1}{{\dfrac{1}{2}}} = \dfrac{2}{1}$

That is the ratio of the area of a parallelogram to the area of the triangle is 2:1

Note:
A parallelogram is a quadrilateral with two pair of equal and opposite sides. All squares, rectangles and rhombus are parallelograms. The area of the rhombus is given by the product of the base and the perpendicular height between two parallel lines.