Question

If a projectile is fired at an angle \[\theta \] with the vertical with velocity $u$, then maximum height attained is given by:
$\begin{align}
  & \text{A}\text{. }\dfrac{{{u}^{2}}\cos \theta }{2g} \\
 & \text{B}\text{. }\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{2g} \\
 & \text{C}\text{. }\dfrac{{{u}^{2}}{{\sin }^{2}}\theta }{g} \\
 & \text{D}\text{. }\dfrac{{{u}^{2}}{{\cos }^{2}}\theta }{2g} \\
\end{align}$

Answer 1

Hint: First draw a rough diagram. Then consider the fact that the vertical component of the initial velocity is zero at maximum height. Then resolve the forces into horizontal and vertical components and use the formula, $s=ut+\dfrac{1}{2}a{{t}^{2}}$.

Complete step by step solution:

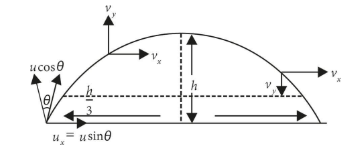
Projectile motion is the motion of an object thrown or projected into the air, subject to only the acceleration of gravity. The object is called a projectile, and its path is called its trajectory. Motion of objects along both perpendicular axes is independent of each other, so they can be analysed individually.

So, resolve the motion into horizontal and vertical components along the x- and y-axes. These axes are perpendicular, so
\[{{A}_{x}}=A\sin \theta \] And \[{{A}_{y}}=A\cos \theta \] where \[{{A}_{x}}\]and \[{{A}_{y}}\] are components of displacement along x-axis.

The magnitudes of the components of the velocity $v$ are \[{{u}_{x}}\text{ }=\text{ u}\sin \theta \] and \[{{u}_{y}}=u\cos \theta \] where u is the magnitude of the initial velocity and θ is the angle with vertical.

Now, according to equation of uniform and accelerated motion,

$s=ut+\dfrac{1}{2}a{{t}^{2}}$
For vertical motion, $a=-g$
And for horizontal motion, $a=0$

Thus, \[{{v}_{x}}\text{ }=u\sin \theta \] for all time during projectile

And \[{{v}_{y}}=u\cos \theta -gt\]
 \[{{A}_{y}}=(u\cos \theta )t-\dfrac{1}{2}g{{t}^{2}}\]
\[{{A}_{x}}=(A\sin \theta )t\]

Now, at maximum height, component of vertical velocity equals to zero,

\[\begin{align}
  & {{v}_{y}}=u\cos \theta -gt=0 \\
 & u\cos \theta =gt \\
 & t=\dfrac{u\cos \theta }{g} \\
\end{align}\]

Height (maximum) = \[{{A}_{y}}\]at \[t=\dfrac{u\cos \theta }{g}\],

\[\begin{align}
  & {{A}_{y}}=(u\cos \theta )t-\dfrac{1}{2}g{{t}^{2}} \\
 & {{A}_{y}}=(u\cos \theta )\dfrac{u\cos \theta }{g}-\dfrac{1}{2}g{{(\dfrac{u\cos \theta }{g})}^{2}} \\
 & {{A}_{y}}=\dfrac{{{u}^{2}}{{\cos }^{2}}\theta }{g}-\dfrac{{{u}^{2}}{{\cos }^{2}}\theta }{2g} \\
 & {{A}_{y}}=\dfrac{{{u}^{2}}{{\cos }^{2}}\theta }{2g} \\
\end{align}\]

Thus, maximum height reached is \[\dfrac{{{u}^{2}}{{\cos }^{2}}\theta }{2g}\] hence option D is correct.

Additional Information:
Suppose that a projectile of mass m is launched, at t=0, from ground level, making an angle \[\theta \] to the horizontal. Suppose, further, that, in addition to the force of gravity, the projectile is subject to an air resistance force which acts in the opposite direction to its instantaneous direction of motion, and whose magnitude is directly proportional to its instantaneous speed. This is not a particularly accurate model of the drag force due to air resistance, the magnitude of the drag force is typically proportional to the square of the speed but it does lead to tractable equations of motion.
We thus conclude that if air resistance is significant then it causes the horizontal range of the projectile to scale linearly, rather than quadratically, with the launch velocity. Moreover, the maximum horizontal range is achieved with a launch angle which is much shallower than the standard result.

Note: It is important to set up a coordinate system when analysing projectile motion. One part of defining the coordinate system is to define an origin for the x and y positions. Often, it is convenient to choose the initial position of the object as the origin such that \[{{x}_{0}}=0\]and \[{{y}_{0}}=0\]. It is also important to define the positive and negative directions in the x and y directions. Typically, we define the positive vertical direction as upwards, and the positive horizontal direction is usually the direction of the object’s motion.