Question

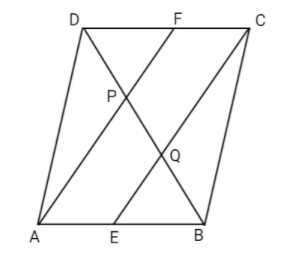
If a parallelogram $ABCD,E$ and $F$ are the mid-points of sides $AB$ and $CD$ respectively. Show that the line segments $AF$ and $EC$ trisect the diagonal $BD$.

Answer 1

Hint: Here we will proceed by using the conversion of midpoints theorem that is the line through the midpoint of one side of a triangle, parallel to another side bisect the third side then by applying the given conditions we will get our answer.

Complete step-by-step answer:
Parallelogram- A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram.
Given –
$ABCD$ is a parallelogram. $E$ and $F$ are the mid-points of sides $AB$ and $CD$ respectively.
To show : Line segments $AF$ and $EC$ trisect the diagonal $BD$.
Proof,
$ABCD$ is a parallelogram
Therefore, $AB$ is parallel to $CD$
Also, $AE$ is parallel to $FC$ (Parts of parallel lines are parallel)
Now,
$AB = CD$ (Opposite sides of parallelogram $ABCD$ )
$\dfrac{1}{2}AB = \dfrac{1}{2}CD$
$AE = FC$ ($E$ and $F$ are midpoints of side $AB$ and $CD$)
Since a pair of opposite sides of a quadrilateral $AECF$ is equal and parallel.
So, $AECF$ is a parallelogram.
Then, $AF$ is parallel to $EC$
$AP$ is parallel to $EQ$ and $FP$ is parallel to $CQ$ (Since opposite sides of a parallelogram are parallel)
Now,
In$\Delta DQC$
$F$ is mid- point of side $DC$ and $FP$ parallel to $CQ$
(as $AF$ is parallel to $EC$)
So, P is the midpoint of $DQ$ (by converse of mid-point theorem)
$DP = DQ$ …..(i)
Similarly,
In $\Delta APB$
$E$ is midpoint of side $AB$ and $EQ$ is parallel to $AP$.
(as $AF$ is parallel to $EC$).
So, $Q$ is the midpoint of $PB$ (by conversion of mid-point theorem)
$PQ = QB$…(iii)
From equations (i) and (iii)
$PQ = QB = DP$
Hence, the line segments $AF$ and $EC$ trisect the diagonal $BD$.

Note: Whenever we come up with this type of problem, we know that a quadrilateral is a parallelogram if its opposite sides are equal, its opposite angles are equal, diagonals bisect other than by using conversion of mid-point theorem we will get our required answer.