Question

If a matrix has 8 elements, what is the possible number of orders it can have?

Answer 1

Hint: Matrix is a set of numbers which are arranged in fixed rows and columns. In a matrix, Number of rows $ \times $ number of columns = Total number of elements in that matrix. To solve this problem we use a trial and error method. As we have to insert 8 elements in the matrix. so, we select the number of rows and columns and then find the total number of elements in the matrix.

Complete step-by-step answer:
It is given that there are 8 elements in any matrix.
As we know, the number of elements in the matrix will equal the product of elements in row and column.
So, we have to find two numbers whose product will be 8.
Like, \[1 \times 8 = 8\]
$2 \times 4 = 8$
$4 \times 2 = 8$
$8 \times 1 = 8$
There are 4 such sets of numbers.
So, we can arrange it in matrix form making its row and column form.
We can arrange 8 elements in the following order:

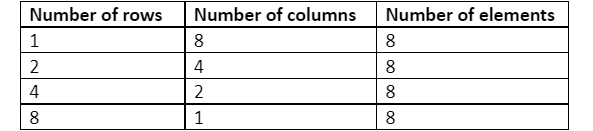
We can arrange a matrix of 8 elements in the above order.
Hence, we can arrange in 4 orders the required matrix.
So, the correct answer is “4”.

Note: Types of Matrices:
(i) Symmetric Matrix
(ii) Skew-Symmetric Matrix
​(iii) Hermitian and skew
(iv) Orthogonal matrix:
(v) Idempotent matrix:
(vi) Involuntary matrix:
(vii) Nilpotent matrix
In every type of matrix the order of matrices is always rows into column.