Question

If a line is drawn parallel to the base of an isosceles triangle to intersect its equal sides, the quadrilateral so formed is cyclic
(a)True
(b)False

Answer 1

Hint: First look at the definition of cyclic quadrilateral. Find relation between angles from isosceles triangle. By the way, the relation between parallel lines and corresponding angles finds the relation of corresponding angles. Now add the both relations you got. Now by this proof the sum of opposite angles are \[{{180}^{\circ }}\]. By this you get the required proof.

Complete step-by-step answer:
Cyclic Quadrilateral: - A quadrilateral which has all four vertices lying on a circle. It is called a cyclic quadrilateral. It is also inscribed quadrilateral. The circle is called circumcircle and vertices are said to concyclic. The opposite angles are supplementary i.e, the sum of opposite angles is \[{{180}^{\circ }}\].
Isosceles triangle: - A triangle whose 2 sides other than base are equal is called an isosceles triangle. Given a condition is written as, a line parallel to base is drawn in an isosceles. Let the parallel line be DE. As ABC is an isosceles triangle, we can say it as:

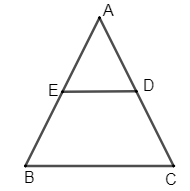
\[\Rightarrow \] AB = AC
As these two sides are equal we get the opposite angles are equal.
By above condition we can say the angles relation as:
\[\Rightarrow \angle ACB=\angle ABC\] - (1)
We need to prove that EDBC is a cyclic quadrilateral.
Given that DE line is a parallel to BC.

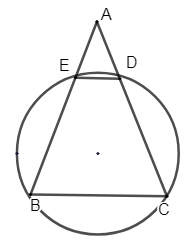
So, line AC is transversal.
A transversal’s corresponding angles are equal.
By applying this to our line AC, we get it as:
\[\Rightarrow \angle ADE=\angle ACB\]
By adding the angle EDC on both sides of equation, we get:
\[\Rightarrow \angle ADE+\angle EDC=\angle EDC+\angle ACB\]
As, ADE + EDC is a straight line sum will be \[{{180}^{\circ }}\].
\[\Rightarrow \angle EDC+\angle ACB={{180}^{\circ }}\]
By substituting the equation (1) here, we get it as:
\[\Rightarrow \angle EDC+\angle ABC={{180}^{\circ }}\]
So, we proved the sum of opposite sides is \[{{180}^{\circ }}\].
Hence proved EDBC is a cyclic quadrilateral.

Note: Be careful while using isosceles condition you must take angles at base to be equal. After getting transversal equation idea to add EDC is derived because we need \[{{180}^{\circ }}\], which is bought only by an angle formed at straight line this idea is very important always remember and use this to generate term \[{{180}^{\circ }}\].