Question

If A is the area of a right angled triangle and b is one of the sides containing the right angle, then the length of the altitude on the hypotenuse is
\[
  A.{\text{ }}\dfrac{{2Ab}}{{\sqrt {{b^2} + 4{A^2}} }} \\
  B.{\text{ }}\dfrac{{2Ab}}{{{b^2} + 4{A^2}}} \\
  C.{\text{ }}\dfrac{{2Ab}}{{\sqrt {{b^4} + 4{A^4}} }} \\
  D.{\text{ }}\dfrac{{2Ab}}{{\sqrt {{b^4} + 4{A^2}} }} \\
 \]

Answer 1

Hint- In order to solve the question start with the basic formula of area of triangle in terms base and altitude and then at the later stage proceed with Pythagoras theorem of some right angled triangle within the figure.

 

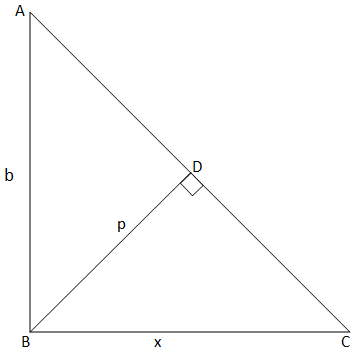
Complete step-by-step answer:
Solve the problem with the help of the figure.
According to the figure and the problem, given that
Height of right angled triangle = b units
Area of the right angled triangle = A sq. units
As we know the formula of triangle in terms of base and altitude is given by:
${\text{Area}} = \dfrac{1}{2} \times {\text{base}} \times {\text{height}}$
So for the given problem
\[
   \Rightarrow A = \dfrac{1}{2} \times x \times b \\
   \Rightarrow x = \dfrac{{2A}}{b} \\
 \]
So, another side (base) of the right angled triangle $ = \dfrac{{2A}}{b}$
According to the Pythagoras theorem for right angled triangles.
\[ \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{base}}} \right)^2} + {\left( {{\text{height}}} \right)^2}\]
So using Pythagoras theorem for right angled triangle ABC
\[
   \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {\dfrac{{2A}}{b}} \right)^2} + {\left( {\text{b}} \right)^2} \\
   \Rightarrow {\left( {{\text{Hypotenuse}}} \right)^2} = \left( {\dfrac{{4{A^2}}}{{{b^2}}}} \right) + {\left( {\text{b}} \right)^2} \\
   \Rightarrow \left( {{\text{Hypotenuse}}} \right) = \sqrt {\left( {\dfrac{{4{A^2}}}{{{b^2}}}} \right) + {{\left( {\text{b}} \right)}^2}} \\
   \Rightarrow \left( {{\text{Hypotenuse}}} \right) = \sqrt {\dfrac{{4{A^2} + {{\left( {\text{b}} \right)}^4}}}{{{b^2}}}} \\
   \Rightarrow \left( {{\text{Hypotenuse}}} \right) = \dfrac{1}{b}\sqrt {{{\left( {\text{b}} \right)}^4} + 4{A^2}} \\
 \]
Now, we have found out the length of hypotenuse. We can also find the area of the right angled triangle ABC by considering side AC as base and the altitude BD to the side AC.
\[
  \because {\text{Area}} = \dfrac{1}{2} \times {\text{base}} \times {\text{height}} \\
   \Rightarrow A = \dfrac{1}{2} \times AC \times BD \\
   \Rightarrow A = \dfrac{1}{2} \times \left( {\dfrac{1}{b}\sqrt {{{\left( {\text{b}} \right)}^4} + 4{A^2}} } \right) \times h \\
   \Rightarrow 2Ab = \sqrt {{{\left( {\text{b}} \right)}^4} + 4{A^2}} \times h \\
   \Rightarrow h = \dfrac{{2Ab}}{{\sqrt {{{\left( {\text{b}} \right)}^4} + 4{A^2}} }} \\
 \]
Therefore, the length of the altitude on the hypotenuse of the right angled triangle is \[\dfrac{{2Ab}}{{\sqrt {{{\left( {\text{b}} \right)}^4} + 4{A^2}} }}\]
So, option D is the correct option.

Note- In order to solve such problems involving the concept of geometry, figure is the utmost priority for easy understanding. Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. Students must remember Pythagoras theorem and the formula for the area of the triangle.