Question

If a given base triangle is described such that the sum of the tangents of the base angles is constant, prove that the locus of the vertices is a parabola.

Answer 1

Hint: We need to take the given condition in co-ordinate plane and use \[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}\] in different triangles

Complete step-by-step answer:
Given that the sum of the tangents of base angles of the triangle is constant. We have to prove that the locus of the vertices is a parabola.

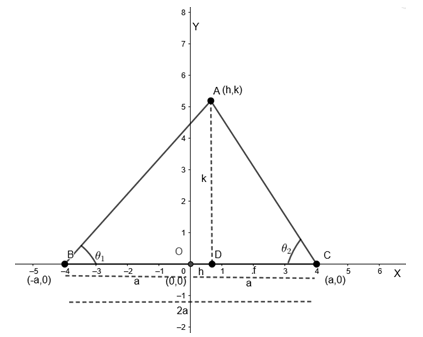
Let the given base of the triangle is BC of length 2a. Also let the coordinates of C be (a, 0) and B be (-a, 0) such that OB = OC = a.
We have to prove that the locus of A is parabola, so let the coordinates of A be (h, k).
Hence, we get OD = h and AD = k.
Also, given that the sum of tangents of angles B and C are constant.
Hence, we get \[\tan {{\theta }_{1}}+\tan {{\theta }_{2}}=C....\left( i \right)\left[ \text{C = constant} \right]\]
We know that \[\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}\]
Therefore, \[\tan {{\theta }_{1}}=\dfrac{AD}{BD}=\dfrac{k}{a+h}\]
And \[\tan {{\theta }_{2}}=\dfrac{AD}{DC}=\dfrac{k}{a-h}\]
Now, we will put these values in equation (i).
We get \[\tan {{\theta }_{1}}+\tan {{\theta }_{2}}=C\]
\[\Rightarrow \dfrac{k}{a+h}+\dfrac{k}{a-h}=C\]
\[\Rightarrow \dfrac{k\left( a-h \right)+k\left( a+h \right)}{\left( a+h \right)\left( a-h \right)}=C\]
Cross Multiplying above equation, we know that,
\[\left( x+y \right)\left( x-y \right)={{x}^{2}}-{{y}^{2}}\]
We get, \[2ka=C\left( {{a}^{2}}-{{h}^{2}} \right)\]
By rearranging the equation, we get,
\[C{{h}^{2}}=C{{a}^{2}}-2ka\]
\[\Rightarrow {{h}^{2}}=\dfrac{-2a}{C}\left[ k-\dfrac{Ca}{2} \right]\]
Replacing h by x and k by y for the locus
\[\Rightarrow {{x}^{2}}=\dfrac{-2a}{C}\left[ y-\dfrac{Ca}{2} \right]\]
which is comparable to parabola.
\[{{\left( x-{{x}_{1}} \right)}^{2}}=-4a\left( y-{{y}_{1}} \right)\]
Hence, we proved that the locus of vertices is a parabola.

Note: Instead of taking arbitrary points, we must take the points in co-ordinate plane like we did in this question to make the question easily solvable. We must rearrange the equation until we get the desired form.