Question

If a complex number z satisfies $\left| z \right| = 1$ and $amp\left( {z - 1} \right) = \dfrac{{2\pi }}{3}$, then
A) $amp\left( {{z^2} + z} \right) = \dfrac{\pi }{2}$
B) $z = - {\omega ^2}$
C) $z = - \omega $
D) $\left| {z - 1} \right| = 1$

Answer 1

Hint:
We can draw the given complex numbers in the plane. Then using the $amp\left( {z - 1} \right)$, we can find the $amp\left( z \right)$. Then we can form a triangle and prove it equilateral. Then we can find the modulus of $z - 1$. Using the $amp\left( z \right)$, we can find the value of z and compare it with ${\omega ^2}$ and $\omega $. Then we can find the value of ${z^2} + z$. Then we can compare with the polar form to find its argument. Then we can compare with the options.

Complete step by step solution:
It is given that $\left| z \right| = 1$ .
So, the point lies on a circle with radius 1 unit, centred at the origin.

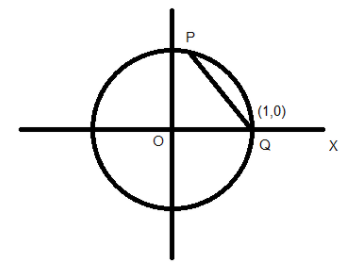
Now consider $z - 1$ .
It is given that $amp\left( {z - 1} \right) = \dfrac{{2\pi }}{3}$
So $z - 1$ lies on a ray originating from the point Q(1,0) that makes an angle of $\dfrac{{2\pi }}{3}$ from the positive x axis.
 $ \Rightarrow \angle PQX = \dfrac{{2\pi }}{3}$
As $\angle PQX$ and $\angle PQO$ forms a linear pair, they are supplementary. So, we can write,
 $ \Rightarrow \angle PQX + \angle PQO = \pi $
On substituting the values, we get,
 $ \Rightarrow \dfrac{{2\pi }}{3} + \angle PQO = \pi $
On rearranging, we get,
 $ \Rightarrow \angle PQO = \pi - \dfrac{{2\pi }}{3}$
On taking the LCM, we get,
 $ \Rightarrow \angle PQO = \dfrac{{3\pi - 2\pi }}{3}$
On simplification we get,
 $ \Rightarrow \angle PQO = \dfrac{\pi }{3}$ … (1)
Let P be the point representing the complex number $z - 1$ . As $\left| z \right| = 1$ , the distance PQ also will be unity.
 $ \Rightarrow PQ = 1$ .. (2)
From the figure, as $z - 1$ , we can write,
 $ \Rightarrow OQ = 1$ .. (3)
Consider the triangle OPQ,
From (1), (2) and (3), the two sides are equal and the included angle is $60^\circ $ .
So OPQ is an equilateral triangle.
As all the sides of an equilateral triangle is equal, we can write,
 $ \Rightarrow OP = OQ = PQ$
OP represents the complex number z and PQ represents the complex number $z - 1$ . From the figure, $PQ = 1$
 $ \Rightarrow \left| z \right| = \left| {z - 1} \right| = 1$
So $\left| {z - 1} \right| = 1$ …. (4).
As OPQ is an equilateral triangle, all the angles will be $60^\circ $
 $ \Rightarrow \angle POQ = \dfrac{\pi }{3}$
So, we can write,
 $ \Rightarrow amp\left( z \right) = \dfrac{\pi }{3}$
We know that complex numbers are represented as $z = r\left( {\cos \theta + i\sin \theta } \right)$ , where r is the modulus as $\theta $ is the argument of the complex number.
So, we can write z as,
 $z = 1\left( {\cos \dfrac{\pi }{3} + i\sin \dfrac{\pi }{3}} \right)$
We know that $\cos \dfrac{\pi }{3} = \dfrac{1}{2}$ and $\sin \dfrac{\pi }{3} = \dfrac{{\sqrt 3 }}{2}$ . On substituting these values, we get,
 $ \Rightarrow z = \dfrac{1}{2} + i\dfrac{{\sqrt 3 }}{2}$
On adding the numerators, we get,
 $ \Rightarrow z = \dfrac{{1 + \sqrt 3 i}}{2}$
On taking a negative sign from the numerator, we get,
 $ \Rightarrow z = - \dfrac{{ - 1 - \sqrt 3 i}}{2}$
We know that ${\omega ^2} = \dfrac{{ - 1 - \sqrt 3 i}}{2}$ . So, we can write,
 $ \Rightarrow z = - {\omega ^2}$ … (5)
Now ${z^2} = {\left( { - {\omega ^2}} \right)^2}$
 $ \Rightarrow {z^2} = {\omega ^4}$
As $\omega $ is cube root of unity, we can write, ${\omega ^4} = \omega $
 $ \Rightarrow {z^2} = \omega $
So, we have,
 $ \Rightarrow {z^2} + z = \omega - {\omega ^2}$
We know that ${\omega ^2} = \dfrac{{ - 1 - \sqrt 3 i}}{2}$ and $\omega = \dfrac{{ - 1 + \sqrt 3 i}}{2}$ . So, we will obtain,
 $ \Rightarrow {z^2} + z = \dfrac{{ - 1 + \sqrt 3 i}}{2} - \left( {\dfrac{{ - 1 - \sqrt 3 i}}{2}} \right)$
On simplification, we get,
 $ \Rightarrow {z^2} + z = \dfrac{{ - 1 + \sqrt 3 i + 1 + \sqrt 3 i}}{2}$
On simplification we get,
 $ \Rightarrow {z^2} + z = \dfrac{{2\sqrt 3 i}}{2}$
Hence, we have,
 $ \Rightarrow {z^2} + z = \sqrt 3 i$
We can express in polar form.
 \[ \Rightarrow {z^2} + z = r\left( {\cos \theta + i\sin \theta } \right)\]
As the real part is zero, we can equate them,
 $ \Rightarrow r\cos \theta = 0$
Dividing by r we get,
 $ \Rightarrow \cos \theta = 0$
On taking inverse of cos we get,
 $ \Rightarrow \theta = {\cos ^{ - 1}}0$
As ${\cos ^{ - 1}}0 = \dfrac{\pi }{2}$ , so we get,
 $ \Rightarrow \theta = \dfrac{\pi }{2}$
So, we can write, $amp\left( {{z^2} + z} \right) = \dfrac{\pi }{2}$ …. (5).
So, from (3), (4), and (5), we can say that,
Options A, B and D are correct.

So, the correct options are,
Option A, which is $amp\left( {{z^2} + z} \right) = \dfrac{\pi }{2}$
Option B, which is $z = - {\omega ^2}$
Option D, which is $\left| {z - 1} \right| = 1$.

Note:
Any complex number can be represented as a point in a plane. The modulus of the complex number gives the distance from the origin to the complex number and the argument gives the angle that the complex number makes with the positive x axis when joined with the origin. $\omega $ and ${\omega ^2}$ are the cube roots of unity, they are conjugate with each other. They have modulus equal to unity and their cube will give unity. So the powers of $\omega $ repeats the values ${\omega ^2}$ , $\omega $ and 1. We used this property to simplify the expression in the last part of the question. We must take care of the negative signs while taking them outside the bracket.