Question

If a circle of unit radius is divided into two parts by an arc of another circle subtending an angle ${{60}^{\circ }}$ on the circumference of the first circle, then the length of the chord is \[\]
A. $\sqrt{3}$\[\]
B. $\dfrac{1}{2}$\[\]
C.1\[\]
D.$\sqrt{2}$\[\]

Answer 1

Hint: We denote the centre as O, the points of intersection both circle as A,B and the point on circumference as C. OD is perpendicular on AB. We find the length of the chord AB with central angle twice the inscribed angle$\angle AOB=2\times \angle ACB=2\times {{60}^{\circ }}$. We use the property of the isosceles triangle to have $\angle AOD=\angle BOD={{60}^{\circ }},AD=BD$. We take sine of angle $\angle AOD$ to get $AD$. \[\]

Complete step by step answer:
Let us denote the centre of the unit circle as O and the points of intersection of circle of unit radius with the other circle as $A,B$. Let us consider the intercepted arc AB as less than semicircle. Let C be any point on the circumference. Since intercepted arc less than semicircle will only subtend an obtuse angle C will not lie on intercepted arc AB. We drop perpendicular OD on AB. So we have the diagram as\[\]
 

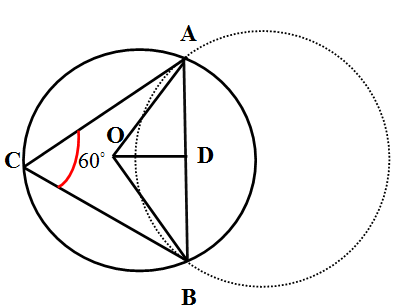
We know that the central angle subtended by an arc at the centre is twice the inscribed angle. Here $\angle ACB$ is an inscribed angle of arc AB with measure given to us as $\angle ACB={{60}^{\circ }}$. So the central angle $\angle AOB$ will have the measure
\[\angle AOB=2\times \angle ACB=2\times {{60}^{\circ }}={{120}^{\circ }}\]
Now we observe the triangle AOB where the lengths of radii are given to us as $OA=OB=1$. Here AOB is an isosceles triangle whose perpendicular from apex O that is AD will bisect the angle at O and the opposite AB. So we have
\[\begin{align}
  & \angle AOD=\angle BOD=\dfrac{{{120}^{\circ }}}{2}={{60}^{\circ }} \\
 & AD=BD=\dfrac{AB}{2} \\
\end{align}\]
So in triangle AOD we have
\[\begin{align}
  & \sin \left( \angle AOD \right)=\dfrac{AD}{OA} \\
 & \Rightarrow \sin \left( {{60}^{\circ }} \right)=\dfrac{AD}{1} \\
 & \Rightarrow AD=1\cdot \sin {{60}^{\circ }}=1\times \dfrac{\sqrt{3}}{2} \\
 & \Rightarrow AD=\dfrac{\sqrt{3}}{2} \\
\end{align}\]
So we have the required length of the chord as ;
\[AB=AD+BD=2AD=2\times \dfrac{\sqrt{3}}{2}=\sqrt{3}\]

So the correct option is A.

Note:
We can similarly solve using inscribed angle and central angle relation to find an intercepted arc AB larger than a semi-circle. We should remember that the sine an angle in a right angled triangle is the ratio of lengths of opposite sides to hypotenuses. We should remember that median and altitude are the same in an isosceles triangle passing through apex.