If a circle and the rectangular hyperbola $xy={{c}^{2}}$ meet in the four points ${{t}_{1}},{{t}_{2}},{{t}_{3}}\And {{t}_{4}}$ then:
(a)${{t}_{1}}{{t}_{2}}{{t}_{3}}{{t}_{4}}=1$
(b)The arithmetic mean of the four points bisects the distance between the centers of the two curves.
(c) The geometric mean of the four points bisects the distance between the centers of the two curves.
(d)The centre of the circle through the points ${{t}_{1}},{{t}_{2}},{{t}_{3}}$ is:
$\left\{ \dfrac{c}{2}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+\dfrac{1}{{{t}_{1}}{{t}_{2}}{{t}_{3}}} \right),\dfrac{c}{2}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+{{t}_{1}}{{t}_{2}}{{t}_{3}} \right) \right\}$
Answer
Verified514.2k+ views
Hint: We know that the general equation of a circle is equal to ${{x}^{2}}+{{y}^{2}}-2gx-2fy+k=0$ here centre of the circle as $\left( g,f \right)$. Now, let us assume any point on the hyperbola as $\left( ct,\dfrac{c}{t} \right)$. This point will pass through the circle because it is given in the above that a circle is cutting a hyperbola in 4 distinct points so we are going to satisfy this point $\left( ct,\dfrac{c}{t} \right)$ in the equation of a circle. Then we will get the 4-degree equation in “t” and then we will write the sum of the roots, the sum of the roots taken two at a time, taken three at a time, and at last the product of roots. By doing so, we will get a relation between ${{t}_{1}},{{t}_{2}},{{t}_{3}}\And {{t}_{4}}$. Then, we can easily solve the options given above.
Complete step-by-step solution:
In the below, we have drawn a rectangular hyperbola $xy={{c}^{2}}$ in such a way that it is cutting by a circle with centre O in 4 distinct points ${{t}_{1}},{{t}_{2}},{{t}_{3}}\And {{t}_{4}}$.
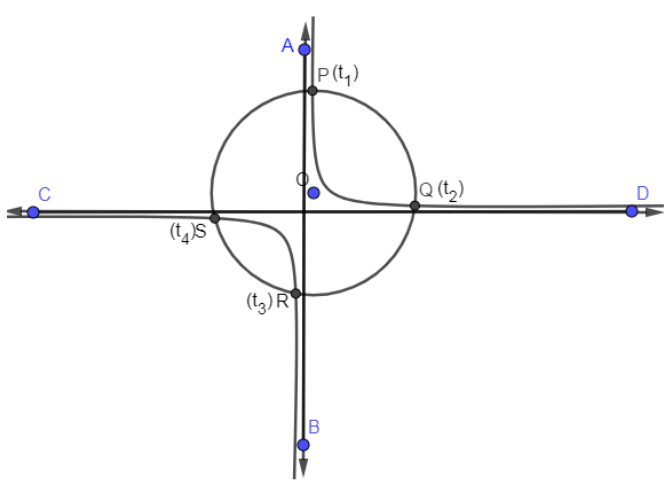
As you can see that we have shown 4 distinct points by P, Q, R and S. Now, let us write the standard equation of circle:
${{x}^{2}}+{{y}^{2}}-2gx-2fy+k=0$
The centre of the circle is O$\left( g,f \right)$. Now, any point on the hyperbola is of the form $\left( ct,\dfrac{c}{t} \right)$ and then we are going to satisfying this point $\left( ct,\dfrac{c}{t} \right)$ in the standard equation of the circle we get,
$\begin{align}
& {{\left( ct \right)}^{2}}+{{\left( \dfrac{c}{t} \right)}^{2}}-2g\left( ct \right)-2f\left( \dfrac{c}{t} \right)+k=0 \\
& \Rightarrow {{c}^{2}}{{t}^{2}}+\dfrac{{{c}^{2}}}{{{t}^{2}}}-2gct-2\dfrac{fc}{t}+k=0 \\
\end{align}$
Taking ${{t}^{2}}$ as a L.C.M in the above equation we get,
$\begin{align}
& \dfrac{{{c}^{2}}{{t}^{4}}+{{c}^{2}}-2gc{{t}^{3}}-2fct+k{{t}^{2}}}{{{t}^{2}}}=0 \\
& \Rightarrow {{c}^{2}}{{t}^{4}}+{{c}^{2}}-2gc{{t}^{3}}-2fct+k{{t}^{2}}=0 \\
\end{align}$
Dividing ${{c}^{2}}$ on both the sides we get,
$\begin{align}
& \dfrac{{{c}^{2}}{{t}^{4}}+{{c}^{2}}-2gc{{t}^{3}}-2fct+k{{t}^{2}}}{{{c}^{2}}}=0 \\
& \Rightarrow {{t}^{4}}+1-2\dfrac{g{{t}^{3}}}{c}-2\dfrac{ft}{c}+\dfrac{k{{t}^{2}}}{{{c}^{2}}}=0 \\
& \Rightarrow {{t}^{4}}-2\dfrac{g{{t}^{3}}}{c}+\dfrac{k{{t}^{2}}}{{{c}^{2}}}-2\dfrac{ft}{c}+1=0 \\
\end{align}$
The above equation is the equation in “t” with degree 4 so it has 4 roots. Now, these 4 roots are:
${{t}_{1}},{{t}_{2}},{{t}_{3}}\And {{t}_{4}}$
Sum of the roots of the equation:
${{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}}=2\dfrac{g}{c}$ …….. Eq. (1)
Sum of the roots taken three at a time:
${{t}_{1}}{{t}_{2}}{{t}_{3}}+{{t}_{2}}{{t}_{3}}{{t}_{1}}+{{t}_{3}}{{t}_{1}}{{t}_{2}}=\dfrac{2f}{c}$………… Eq. (2)
Product of the roots is equal to:
${{t}_{1}}{{t}_{2}}{{t}_{3}}{{t}_{4}}=1$ ………. Eq. (3)
From eq. (3), option (a) is correct.
The arithmetic mean of the four points ${{t}_{1}},{{t}_{2}},{{t}_{3}}\And {{t}_{4}}$ is equal to:
$\begin{align}
& \left( \dfrac{c\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}} \right)}{4},\dfrac{c}{4}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{1}{{{t}_{4}}} \right) \right) \\
& =\left( \dfrac{c\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}} \right)}{4},\dfrac{c}{4}\left( \dfrac{{{t}_{2}}{{t}_{3}}{{t}_{4}}+{{t}_{3}}{{t}_{4}}{{t}_{1}}+{{t}_{4}}{{t}_{1}}{{t}_{2}}}{{{t}_{1}}{{t}_{2}}{{t}_{3}}{{t}_{4}}} \right) \right) \\
\end{align}$
Using the eq. (1, 2 and 3) in the above expression we get,
$\begin{align}
& \left( \dfrac{c}{4}\left( \dfrac{2g}{c} \right),\dfrac{c}{4}\left( \dfrac{2f}{c} \right) \right) \\
& =\left( \dfrac{g}{2},\dfrac{f}{2} \right) \\
\end{align}$
Now, we know that, centre of the hyperbola is (0, 0) and centre of circle is (g, f) then the midpoint of these two points is equal to:
We know that if we have two points say $\left( {{x}_{1}},{{y}_{1}} \right)\And \left( {{x}_{2}},{{y}_{2}} \right)$ then the midpoint of these two points is equal to:
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
Using this midpoint formula, we are going to find the midpoint of (0, 0) and (g, f).
$\begin{align}
& \left( \dfrac{g+0}{2},\dfrac{f+0}{2} \right) \\
& =\left( \dfrac{g}{2},\dfrac{f}{2} \right) \\
\end{align}$
From the above, we can say that the arithmetic mean of four points bisects the centre of the two curves.
Hence, option (b) is also correct.
From eq. (3) we can write:
$\begin{align}
& {{t}_{1}}{{t}_{2}}{{t}_{3}}{{t}_{4}}=1 \\
& \Rightarrow {{t}_{4}}=\dfrac{1}{{{t}_{1}}{{t}_{2}}{{t}_{3}}}......Eq.(4) \\
\end{align}$
Now, using the arithmetic mean of four points and the bisection of centres of two curves we can write:
$\dfrac{g}{2}=\dfrac{c}{4}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}} \right)$
Multiplying 2 on both the sides we get,
$\begin{align}
& \dfrac{g}{2}\times 2=\dfrac{c}{4}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}} \right)\times 2 \\
& \Rightarrow g=\dfrac{c}{2}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}} \right)........Eq.(5) \\
\end{align}$
$\dfrac{f}{2}=\dfrac{c}{4}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{1}{{{t}_{4}}} \right)$
Multiplying 2 on both the sides we get,
$\begin{align}
& \dfrac{f}{2}\times 2=\dfrac{c}{4}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{1}{{{t}_{4}}} \right)\times 2 \\
& \Rightarrow f=\dfrac{c}{2}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{1}{{{t}_{4}}} \right)........Eq.(6) \\
\end{align}$
Now, using eq. (4) in eq. (5) and eq. (6) we get,
$g=\dfrac{c}{2}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+\dfrac{1}{{{t}_{1}}{{t}_{2}}{{t}_{3}}} \right)$
$f=\dfrac{c}{2}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{{{t}_{1}}{{t}_{2}}{{t}_{3}}}{1} \right)$
And we know that, centre of the circle is (g, f) so we can write the centre of the circle as:
$\left( \dfrac{c}{2}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+\dfrac{1}{{{t}_{1}}{{t}_{2}}{{t}_{3}}} \right),\dfrac{c}{2}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{{{t}_{1}}{{t}_{2}}{{t}_{3}}}{1} \right) \right)$
Hence, option (d) is also correct.
From the above, the correct options are (a), (b), and (d).
Note: The mistake that could happen in this problem is that while reading the question you might have drawn the figure in such a way that the center of the rectangular hyperbola and circle is coinciding. This is a very common mistake that could happen that’s why in the above solution; we have drawn the center of circle O which is not coinciding with the hyperbola to avoid this mistake. In the below figure, you can see the center of the circle as O.
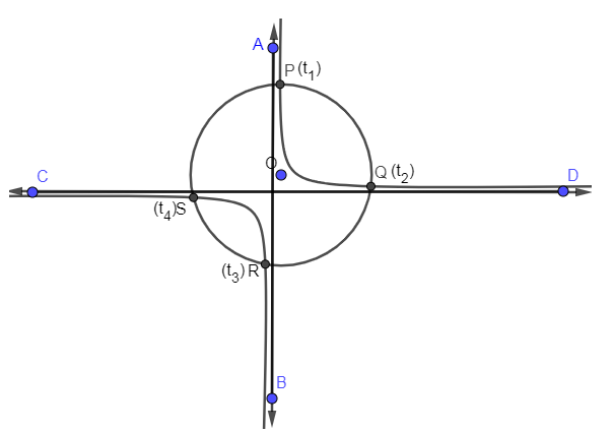
Complete step-by-step solution:
In the below, we have drawn a rectangular hyperbola $xy={{c}^{2}}$ in such a way that it is cutting by a circle with centre O in 4 distinct points ${{t}_{1}},{{t}_{2}},{{t}_{3}}\And {{t}_{4}}$.
As you can see that we have shown 4 distinct points by P, Q, R and S. Now, let us write the standard equation of circle:
${{x}^{2}}+{{y}^{2}}-2gx-2fy+k=0$
The centre of the circle is O$\left( g,f \right)$. Now, any point on the hyperbola is of the form $\left( ct,\dfrac{c}{t} \right)$ and then we are going to satisfying this point $\left( ct,\dfrac{c}{t} \right)$ in the standard equation of the circle we get,
$\begin{align}
& {{\left( ct \right)}^{2}}+{{\left( \dfrac{c}{t} \right)}^{2}}-2g\left( ct \right)-2f\left( \dfrac{c}{t} \right)+k=0 \\
& \Rightarrow {{c}^{2}}{{t}^{2}}+\dfrac{{{c}^{2}}}{{{t}^{2}}}-2gct-2\dfrac{fc}{t}+k=0 \\
\end{align}$
Taking ${{t}^{2}}$ as a L.C.M in the above equation we get,
$\begin{align}
& \dfrac{{{c}^{2}}{{t}^{4}}+{{c}^{2}}-2gc{{t}^{3}}-2fct+k{{t}^{2}}}{{{t}^{2}}}=0 \\
& \Rightarrow {{c}^{2}}{{t}^{4}}+{{c}^{2}}-2gc{{t}^{3}}-2fct+k{{t}^{2}}=0 \\
\end{align}$
Dividing ${{c}^{2}}$ on both the sides we get,
$\begin{align}
& \dfrac{{{c}^{2}}{{t}^{4}}+{{c}^{2}}-2gc{{t}^{3}}-2fct+k{{t}^{2}}}{{{c}^{2}}}=0 \\
& \Rightarrow {{t}^{4}}+1-2\dfrac{g{{t}^{3}}}{c}-2\dfrac{ft}{c}+\dfrac{k{{t}^{2}}}{{{c}^{2}}}=0 \\
& \Rightarrow {{t}^{4}}-2\dfrac{g{{t}^{3}}}{c}+\dfrac{k{{t}^{2}}}{{{c}^{2}}}-2\dfrac{ft}{c}+1=0 \\
\end{align}$
The above equation is the equation in “t” with degree 4 so it has 4 roots. Now, these 4 roots are:
${{t}_{1}},{{t}_{2}},{{t}_{3}}\And {{t}_{4}}$
Sum of the roots of the equation:
${{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}}=2\dfrac{g}{c}$ …….. Eq. (1)
Sum of the roots taken three at a time:
${{t}_{1}}{{t}_{2}}{{t}_{3}}+{{t}_{2}}{{t}_{3}}{{t}_{1}}+{{t}_{3}}{{t}_{1}}{{t}_{2}}=\dfrac{2f}{c}$………… Eq. (2)
Product of the roots is equal to:
${{t}_{1}}{{t}_{2}}{{t}_{3}}{{t}_{4}}=1$ ………. Eq. (3)
From eq. (3), option (a) is correct.
The arithmetic mean of the four points ${{t}_{1}},{{t}_{2}},{{t}_{3}}\And {{t}_{4}}$ is equal to:
$\begin{align}
& \left( \dfrac{c\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}} \right)}{4},\dfrac{c}{4}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{1}{{{t}_{4}}} \right) \right) \\
& =\left( \dfrac{c\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}} \right)}{4},\dfrac{c}{4}\left( \dfrac{{{t}_{2}}{{t}_{3}}{{t}_{4}}+{{t}_{3}}{{t}_{4}}{{t}_{1}}+{{t}_{4}}{{t}_{1}}{{t}_{2}}}{{{t}_{1}}{{t}_{2}}{{t}_{3}}{{t}_{4}}} \right) \right) \\
\end{align}$
Using the eq. (1, 2 and 3) in the above expression we get,
$\begin{align}
& \left( \dfrac{c}{4}\left( \dfrac{2g}{c} \right),\dfrac{c}{4}\left( \dfrac{2f}{c} \right) \right) \\
& =\left( \dfrac{g}{2},\dfrac{f}{2} \right) \\
\end{align}$
Now, we know that, centre of the hyperbola is (0, 0) and centre of circle is (g, f) then the midpoint of these two points is equal to:
We know that if we have two points say $\left( {{x}_{1}},{{y}_{1}} \right)\And \left( {{x}_{2}},{{y}_{2}} \right)$ then the midpoint of these two points is equal to:
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
Using this midpoint formula, we are going to find the midpoint of (0, 0) and (g, f).
$\begin{align}
& \left( \dfrac{g+0}{2},\dfrac{f+0}{2} \right) \\
& =\left( \dfrac{g}{2},\dfrac{f}{2} \right) \\
\end{align}$
From the above, we can say that the arithmetic mean of four points bisects the centre of the two curves.
Hence, option (b) is also correct.
From eq. (3) we can write:
$\begin{align}
& {{t}_{1}}{{t}_{2}}{{t}_{3}}{{t}_{4}}=1 \\
& \Rightarrow {{t}_{4}}=\dfrac{1}{{{t}_{1}}{{t}_{2}}{{t}_{3}}}......Eq.(4) \\
\end{align}$
Now, using the arithmetic mean of four points and the bisection of centres of two curves we can write:
$\dfrac{g}{2}=\dfrac{c}{4}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}} \right)$
Multiplying 2 on both the sides we get,
$\begin{align}
& \dfrac{g}{2}\times 2=\dfrac{c}{4}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}} \right)\times 2 \\
& \Rightarrow g=\dfrac{c}{2}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+{{t}_{4}} \right)........Eq.(5) \\
\end{align}$
$\dfrac{f}{2}=\dfrac{c}{4}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{1}{{{t}_{4}}} \right)$
Multiplying 2 on both the sides we get,
$\begin{align}
& \dfrac{f}{2}\times 2=\dfrac{c}{4}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{1}{{{t}_{4}}} \right)\times 2 \\
& \Rightarrow f=\dfrac{c}{2}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{1}{{{t}_{4}}} \right)........Eq.(6) \\
\end{align}$
Now, using eq. (4) in eq. (5) and eq. (6) we get,
$g=\dfrac{c}{2}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+\dfrac{1}{{{t}_{1}}{{t}_{2}}{{t}_{3}}} \right)$
$f=\dfrac{c}{2}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{{{t}_{1}}{{t}_{2}}{{t}_{3}}}{1} \right)$
And we know that, centre of the circle is (g, f) so we can write the centre of the circle as:
$\left( \dfrac{c}{2}\left( {{t}_{1}}+{{t}_{2}}+{{t}_{3}}+\dfrac{1}{{{t}_{1}}{{t}_{2}}{{t}_{3}}} \right),\dfrac{c}{2}\left( \dfrac{1}{{{t}_{1}}}+\dfrac{1}{{{t}_{2}}}+\dfrac{1}{{{t}_{3}}}+\dfrac{{{t}_{1}}{{t}_{2}}{{t}_{3}}}{1} \right) \right)$
Hence, option (d) is also correct.
From the above, the correct options are (a), (b), and (d).
Note: The mistake that could happen in this problem is that while reading the question you might have drawn the figure in such a way that the center of the rectangular hyperbola and circle is coinciding. This is a very common mistake that could happen that’s why in the above solution; we have drawn the center of circle O which is not coinciding with the hyperbola to avoid this mistake. In the below figure, you can see the center of the circle as O.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success
Master Class 11 Accountancy: Engaging Questions & Answers for Success
Master Class 11 English: Engaging Questions & Answers for Success
Master Class 11 Social Science: Engaging Questions & Answers for Success
Master Class 11 Biology: Engaging Questions & Answers for Success
Master Class 11 Physics: Engaging Questions & Answers for Success
Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE
Difference Between Prokaryotic Cells and Eukaryotic Cells
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE
Draw a diagram of nephron and explain its structur class 11 biology CBSE
Explain zero factorial class 11 maths CBSE