Question

If a and b are unit vectors and |a+b| = 1, then |a-b| is equal to
[a] $\sqrt{2}$
[b] 1
[c] $\sqrt{5}$
[d] $\sqrt{3}$

Answer 1

Hint: Observe that the vector a+b and a-b are orthogonal to each other. Use Pythagoras theorem in triangle BCD and hence find |a-b|. Alternatively use ${{\left| \mathbf{a} \right|}^{2}}=\mathbf{a}\cdot \mathbf{a}$. Apply the formula for $\left| \mathbf{a}+\mathbf{b} \right|$ and $\left| \mathbf{a}-\mathbf{b} \right|$ and add the two results. Hence find the value of $\left| \mathbf{a}-\mathbf{b} \right|$.

Complete step-by-step answer:

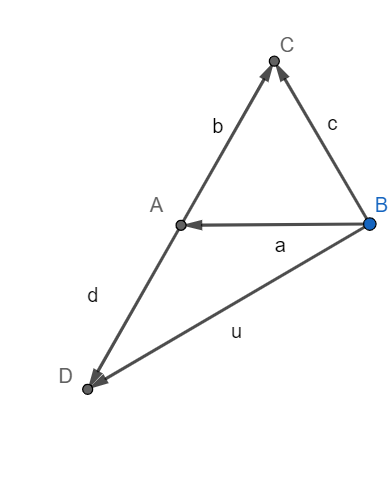
Here AD = -b
Sine AB = AD = 1 unit, we have $\angle ABD=\angle ADB$.
Also, we have $\angle CAB$ is an exterior angle of triangle ABD.
Hence $\angle CAB=\angle ADB+\angle ABD=2\angle ABD$
In triangle ABC, we have AB = AC. Hence $\angle ABC=\angle ACB$
Hence by angle sum property of a triangle, we have
$\begin{align}
  & \angle CAB+\angle ABC+\angle ACB=180{}^\circ \\
 & \Rightarrow \angle CAB=180{}^\circ -2\angle ABC \\
\end{align}$
Hence, we have
$\begin{align}
  & 2\angle ABD=180{}^\circ -2\angle ABC \\
 & \Rightarrow 2\left( \angle ABD+\angle ABC \right)=180{}^\circ \\
 & \Rightarrow 2\left( \angle CBD \right)=180{}^\circ \\
 & \Rightarrow \angle CBD=90{}^\circ \\
\end{align}$
Hence triangle CBD is a right-angled triangle right angled at B.
Now in triangle CBD, by Pythagora’s theorem, we have
$B{{C}^{2}}+B{{D}^{2}}=C{{D}^{2}}$
Since BC = BA+AC, we have
c = a+b.
Hence, BC = 1 unit, since |a+b|=1.
 Also DC = |a|+|-a|=2|a|=2.
Hence, we have
$\begin{align}
  & 1+B{{D}^{2}}=4 \\
 & \Rightarrow B{{D}^{2}}=3 \\
 & \Rightarrow BD=\sqrt{3} \\
\end{align}$
Now, we have
BD = a+d.
Since d = -b, we have
BD = a-b.
Hence |a-b| $=\sqrt{3}$
Hence option [d] is correct.

Note: [1] Alternate proof of $\angle CBD=90{}^\circ $
As is evident from the diagram $\angle CBD$ is the angle between the vector u and c.
Hence we have $\cos \left( \angle CBD \right)=\dfrac{\mathbf{u}\cdot \mathbf{c}}{\left| \mathbf{u} \right|\left| \mathbf{c} \right|}=\dfrac{\left( \mathbf{a}-\mathbf{b} \right)\left( \mathbf{a}+\mathbf{b} \right)}{\left| \mathbf{a}-\mathbf{b} \right|\left| \mathbf{a}+\mathbf{b} \right|}=\dfrac{{{\left| \mathbf{a} \right|}^{2}}-{{\left| \mathbf{b} \right|}^{2}}+\mathbf{a}\cdot \mathbf{b}-\mathbf{a}\cdot \mathbf{b}}{\left| \mathbf{a}-\mathbf{b} \right|\left| \mathbf{a}+\mathbf{b} \right|}=\dfrac{1-1}{\left| \mathbf{a}-\mathbf{b} \right|\left| \mathbf{a}+\mathbf{b} \right|}=0$
Hence we have $\angle CBD=90{}^\circ $
[2] Alternative solution: Best Method
We know that
${{\left| \mathbf{a} \right|}^{2}}=\mathbf{a}\cdot \mathbf{a}$
Hence, we have
${{\left| \mathbf{a}+\mathbf{b} \right|}^{2}}=\left( \mathbf{a}+\mathbf{b} \right)\cdot \left( \mathbf{a}+\mathbf{b} \right)=\mathbf{a}\cdot \mathbf{a}+\mathbf{a}\cdot \mathbf{b}+\mathbf{b}\cdot \mathbf{a}+\mathbf{b}\cdot \mathbf{b}={{\left| \mathbf{a} \right|}^{2}}+{{\left| \mathbf{b} \right|}^{2}}+2\mathbf{a}\cdot \mathbf{b}=2+2\mathbf{a}\cdot \mathbf{b}$
Also, we have
${{\left| \mathbf{a}-\mathbf{b} \right|}^{2}}=\left( \mathbf{a}-\mathbf{b} \right)\cdot \left( \mathbf{a}-\mathbf{b} \right)=\mathbf{a}\cdot \mathbf{a}-\mathbf{a}\cdot \mathbf{b}-\mathbf{b}\cdot \mathbf{a}+\mathbf{b}\cdot \mathbf{b}={{\left| \mathbf{a} \right|}^{2}}+{{\left| \mathbf{b} \right|}^{2}}-2\mathbf{a}\cdot \mathbf{b}=2-2\mathbf{a}\cdot \mathbf{b}$
Adding, we get
${{\left| \mathbf{a}-\mathbf{b} \right|}^{2}}+{{\left| \mathbf{a}+\mathbf{b} \right|}^{2}}=4$
Given that |a+b| = 1, we get
$\begin{align}
  & {{\left| \mathbf{a}-\mathbf{b} \right|}^{2}}+1=4 \\
 & \Rightarrow {{\left| \mathbf{a}-\mathbf{b} \right|}^{2}}=3 \\
 & \Rightarrow \left| \mathbf{a}-\mathbf{b} \right|=\sqrt{3} \\
\end{align}$
which is the same as obtained above.