Question

If $A$ and $B$ are two subsets $X$ then $\left( A\bigcap \left( X-B \right) \right)\bigcup B=$ \[\]
A.$A\bigcup B$\[\]
B.$A\bigcap B$\[\]
C.$A$\[\]
D. $B$\[\]

Answer 1

Hint: We recall the definition of union $x\in A\text{ or }x\in B\Rightarrow x\in A\bigcup B$, intersection $x\in A\text{ and }x\in B\Rightarrow x\in A\bigcap B$, compliments $x\in {{A}^{c}}\Rightarrow x\in X\text{ and }x\notin A$and exclusion of sets $x\in A-B\Rightarrow x\in A\text{ and }x\notin B$ for some arbitrary element $x$. We assume $x\in \left( A\bigcap \left( X-B \right) \right)\bigcup B$ and simplify using the definitions.

Complete step-by-step answer:
We know that of an element $x$ belongs to $A$ we can write as $x\in A$. If there is another set $B$ such that $x\in B$ then we define the union of sets as
\[x\in A\text{ or }x\in B\Rightarrow x\in A\bigcup B\]
Similarly we define the intersection of sets as,
\[x\in A\text{ and }x\in B\Rightarrow x\in A\bigcap B\]
If $X$ is a set such that $A$ and $B$ are two subsets $X$ then compliments are defined as ${{A}^{c}}=X-A,{{B}^{c}}=X-B$. If we take an arbitrary element $x$ then we have
 \[\begin{align}
  & x\in {{A}^{c}}\Rightarrow x\in X\text{ and }x\notin A \\
 & x\in {{B}^{c}}\Rightarrow x\in X\text{ and }x\notin B \\
\end{align}\]
We define the exclusion of set $B$ from $A$ as
\[\begin{align}
  & x\in A-B\Rightarrow x\in A\text{ and }x\notin B \\
 & \Rightarrow x\in A-B\Rightarrow x\in A\text{ and }x\in {{B}^{c}} \\
\end{align}\]

 We are given in the question the set$\left( A\bigcap \left( X-B \right) \right)\bigcup B$. Let us assume for some arbitrary element $x$ such that,
\[x\in \left( A\bigcap \left( X-B \right) \right)\bigcup B\]
We use the definition of union of sets and have
\[\Rightarrow x\in A\bigcap \left( X-B \right)\text{ or }x\in B\]
We use the definition of intersection of sets and have
\[\Rightarrow x\in A\text{ and }x\in X-B\text{ or }x\in B\]
We use the definition of exclusion and have;
\[\begin{align}
  & \Rightarrow x\in A\text{ and }x\in {{B}^{c}}\text{ or }x\in B \\
 & \Rightarrow x\in A-B\text{ or }x\in B \\
 & \Rightarrow x\in A\bigcup B \\
\end{align}\]
So the correct option is A. We can verify the result using Venn diagrams. We represent the set $X$ as a rectangle and the sets $A,B$ as intersecting circles. We shade the region in blue excluding circle B to represent $X-B$.\[\]
 

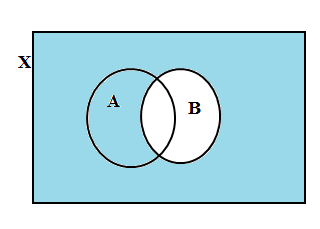
We take its intersection with circle $A$ to find shade the common region to represent $A\bigcap \left( X-B \right)$.\[\]
 

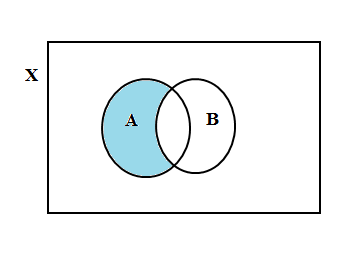
We take the union of $A\bigcap \left( X-B \right)$ and add up the region of circle $B$ and shade the region to represent $\left( A\bigcap \left( X-B \right) \right)\bigcup B$ .\[\]
 

We know that above shaded region is the region represented by the set $A\bigcup B$. \[\]

So, the correct answer is “Option A”.

Note: We must be careful while shading regions for union and intersection. The word ‘arbitrary’ means any element of our choice. $X$ can also be represented as universal for the sets $A$ and $B$. We note that operations union and intersections are distributive. \[\]