Question

 If A and B are two points on a circle such that \[m\left( \overline{AB} \right)=260{}^\circ \]
A possible value for the angle subtended by arc BA at a point on the circle is
A. $100{}^\circ $
B. $75{}^\circ $
C. $50{}^\circ $
D. $25{}^\circ $

Answer 1

Hint: Angle inscribed by an acr at the centre is double the angle inscribed by the same arc at any point on the circumference of the circle.

Complete Step-by-Step solution:
As we all know, the measure of a complete circle is 360°.
\[\therefore \]\[m\left( circle \right)=360{}^\circ \]
As given in the problem, Measure of Arc AB is 260°
i.e. \[m\left( \overline{AB} \right)=260{}^\circ \]
We will solve this problem through a simple concept,
Concept: Arc Measure is the measure of angle made by it at the centre of a circle.
Refering to the figure and above concept we can say that,
reflex of angle AOB = \[m\left( \overline{AB} \right)=260{}^\circ \]
Now, to find the Measure of Arc BA i.e. is simply the measure of angle BOA.

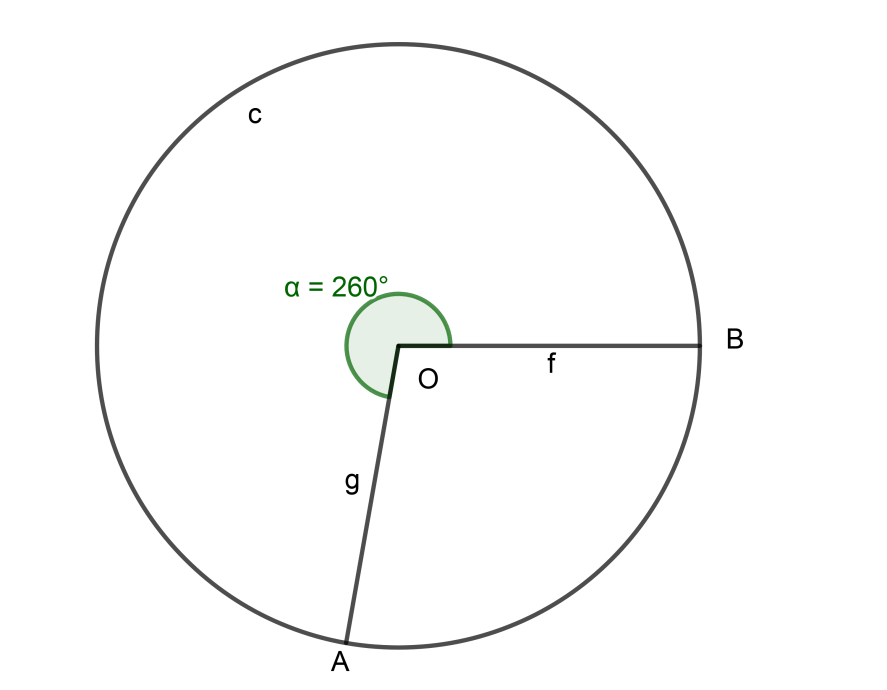
From above figure it is clear that,
\[m\left( circle \right)\]=reflex of\[\angle AOB+\angle AOB\]
\[360{}^\circ =m\left( \overline{AB} \right)+m\left( \overline{BA} \right)\]
\[360{}^\circ =260{}^\circ +m\left( \overline{BA} \right)\]
\[m\left( \overline{BA} \right)=360{}^\circ -260{}^\circ \]
\[m\left( \overline{BA} \right)=100{}^\circ \]………………………………………………. (1)
Here half of the answer is covered. Now if we read the question carefully we will see that they have asked to find the angle made by arc BA at a point on a circle and not at the centre.

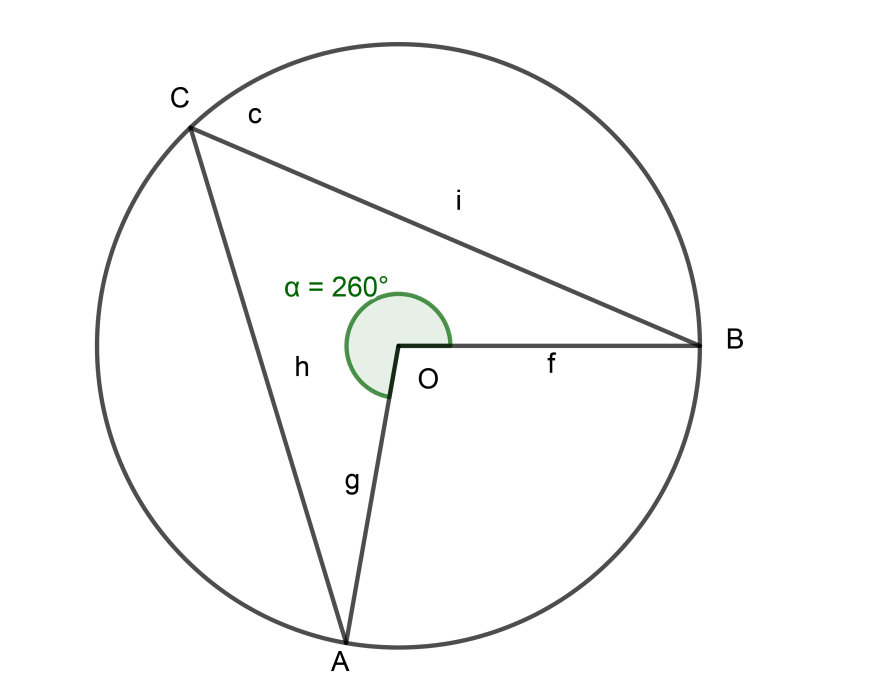
To find that let’s take any point C on Arc AB and construct two segments AC and BC at a point C on the circumference of the circle.
Therefore, \[\angle BCA\] be any angle made by the arc BA at any point on the circumference of the circle.And to find that angle we should know the concept given below,
Concept:
Angle inscribed by an acr at the centre is double the angle inscribed by the same arc at any point on the circumference of the circle.
Form the above concept we can write that,
\[\angle BOA=2\angle BCA\]…………………………………………………… (2)
Now from (1) we can write,
\[m\left( \overline{BA} \right)=100{}^\circ \]
As we discussed the concept earlier i.e. “Arc Measure is the measure of angle made by it at the centre of circle”
Therefore,
\[m\left( \overline{BA} \right)=\angle BOA\]
\[\therefore m\left( \overline{BA} \right)=\angle BOA=100{}^\circ \]…………………………………………. (3)
If we put the value of equation (3) in equation (2) we will get,
\[100{}^\circ =2\angle BCA\]
\[\therefore \angle BCA=\dfrac{100{}^\circ }{2}\]
\[\therefore \angle BCA=50{}^\circ \]
As we have considered point C as any point on the Arc AB therefore we can say that,
A possible value for the angle subtended by arc BA at a point on the circle is \[50{}^\circ \]
Option C is correct.

Note: Always remember to draw diagrams for this type of problems to avoid confusion.
Read the question carefully as they have asked for the angle made by arc at any point on the circumference of the circle, there are chances that we may confuse and just find the angle made by arc at the centre.