Question

If A and B are arbitrary events, then
A) \[P\left( {A \cap B} \right) \ge P\left( A \right) + P\left( B \right)\]
B) \[P\left( {A \cap B} \right) \le P\left( A \right) + P\left( B \right)\]
C) \[P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)\]
D) None of these.

Answer 1

Hint:
We will draw a Venn-diagram for both the events A and B and we will find \[P\left( A \right)\], \[P\left( B \right)\] and \[P\left( {A \cap B} \right)\] using the Venn-diagram. Then, we will compare \[P\left( A \right) + P\left( B \right)\] and \[P\left( {A \cap B} \right)\] to find the correct option.

Complete step by step solution:
Let’s represent event \[A\] by the 1st circle and event \[B\] by the $2^{\text{nd}}$ circle.

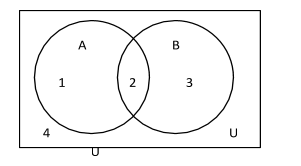
From the figure, we can see that \[P\left( A \right)\] is represented by region 1 and region 2.
\[P\left( A \right) = 1 + 2{\rm{ }}\left( 1 \right)\]
We can also see that \[P\left( B \right)\] is represented by region 2 and region 3.
\[P\left( B \right) = 2 + 3{\rm{ }}\left( 2 \right)\].
\[P\left( {A \cap B} \right)\] means the intersection of\[A\] and \[B\]and is represented by the region which is common to both \[A\] and \[B\]. So, we will represent \[P\left( {A \cap B} \right)\] by region 2.
\[P\left( {A \cap B} \right) = 2{\rm{ }}\left( 3 \right)\].
\[P\left( {A \cup B} \right)\] means the union of\[A\] and \[B\]and is represented by the region that covers both \[A\] and \[B\].
So, we will represent \[P\left( {A \cup B} \right)\] by region 1, region 2 and region 3.
\[P\left( {A \cup B} \right) = 1 + 2 + 3{\rm{ }}\left( 4 \right)\].
Let’s add equation (1) and equation (2).
\[P\left( A \right) + P\left( B \right) = 1 + 2 + 2 + 3\]
Let’s subtract equation (4) from the sum of equation (2) and equation (1).
\[\begin{array}{l}P\left( A \right) + P\left( B \right) - P\left( {A \cup B} \right) = 1 + 2 + 2 + 3 - \left( {1 + 2 + 3} \right)\\P\left( A \right) + P\left( B \right) - P\left( {A \cup B} \right) = 2{\rm{ }}\left( 5 \right)\end{array}\]
Let’s compare equation (5) and equation (3).
\[P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cup B} \right)\]
Let’s add \[P\left( {A \cup B} \right)\] to both sides of the equation.
\[P\left( {A \cap B} \right) + P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\]
We have to add something to \[P\left( {A \cap B} \right)\] to \[P\left( A \right) + P\left( B \right)\]. This means that \[P\left( {A \cap B} \right)\]is smaller than \[P\left( A \right) + P\left( B \right)\]. \[P\left( {A \cap B} \right)\]can also be equal to \[P\left( A \right) + P\left( B \right)\]if value of \[P\left( {A \cup B} \right)\]is 0.
 \[\therefore P\left( {A \cap B} \right) \le P\left( A \right) + P\left( B \right)\].

Option (B) is the correct option.

Note:
We can directly use the formula \[P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right) - P\left( {A \cup B} \right)\] to solve this question. We need to be careful about the fact that \[P\left( {A \cup B} \right)\] is not equal to \[P\left( A \right) + P\left( B \right)\].