Question

If A (3, y) is equidistant from points P (8, – 3) and Q (7, 6), find the value of y and find the distance AQ.

Answer 1

Hint: Equate the distances AP and AQ by using the distance formula to find the distance between any two points \[\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)\] which is \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]. From this find the value of y. Now substitute the value of y in distance AQ to find the value of AQ.
Complete step-by-step answer:
We are given that if A (3, y) is equidistant from points P (8, – 3) and Q (7, 6), then we have to find the value of y and AQ.

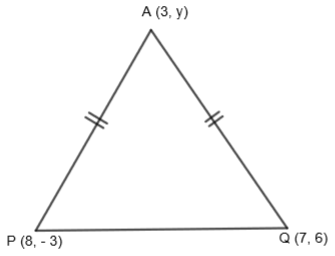
We know the distance between any two points \[M\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }N\left( {{x}_{2}},{{y}_{2}} \right)\] can be found by using the distance formula which is
\[MN=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]
So, by using distance formula, we get the distance between points A (3, y) and P (8, – 3) as
\[AP=\sqrt{{{\left( 8-3 \right)}^{2}}+{{\left( -3-y \right)}^{2}}}\]
\[AP=\sqrt{{{\left( 5 \right)}^{2}}+{{\left( -\left( y+3 \right) \right)}^{2}}}\]
\[AP=\sqrt{25+{{\left( y+3 \right)}^{2}}}....\left( i \right)\]
Again by using distance formula, we get the distance between points A (3, y) and Q (7, 6) as
\[AQ=\sqrt{{{\left( 7-3 \right)}^{2}}+{{\left( 6-y \right)}^{2}}}\]
\[AQ=\sqrt{{{\left( 4 \right)}^{2}}+{{\left( -\left( y-6 \right) \right)}^{2}}}\]
\[AQ=\sqrt{16+{{\left( y-6 \right)}^{2}}}....\left( ii \right)\]
We are given that point A is equidistant from points P and Q. So, we get,
AP = AQ.
By substituting the value of AP and AQ from equation (i) and (ii) respectively, we get,
\[\sqrt{25+{{\left( y+3 \right)}^{2}}}=\sqrt{16+{{\left( y-6 \right)}^{2}}}.....\left( iii \right)\]
By squaring both sides of the above equation, we get,
\[25+{{\left( y+3 \right)}^{2}}=16+{{\left( y-6 \right)}^{2}}\]
By using \[{{\left( a\pm b \right)}^{2}}={{a}^{2}}+{{b}^{2}}\pm 2ab\], we get,
\[25+{{\left( y \right)}^{2}}+{{\left( 3 \right)}^{2}}+2\left( 3 \right)y=16+{{y}^{2}}+{{\left( 6 \right)}^{2}}-2\left( 6 \right)y\]
\[25+{{y}^{2}}+9+6y=16+{{y}^{2}}+36-12y\]
By canceling the like terms and simplifying the above equation, we get,
\[25+9+6y=16+36-12y\]
\[34+6y=52-12y\]
\[6y+12y=52-34\]
\[18y=18\]
\[y=1\]
Now, by substituting the value of y = 1 in equation (ii), we get,
\[AQ=\sqrt{16+{{\left( 1-6 \right)}^{2}}}\]
\[AQ=\sqrt{16+{{\left( -5 \right)}^{2}}}\]
\[AQ=\sqrt{16+25}\]
\[AQ=\sqrt{41}\]
So, we get the value of AQ as \[\sqrt{41}\] and y as 1.

Note: In this question, as it is given that A is equidistant from points P and Q, many students make this mistake of considering A as the midpoint of line PQ and get \[y=\dfrac{6-3}{2}=\dfrac{3}{2}\] which is wrong because if a point is equidistant from 2 other points, it can or cannot be the midpoint. So, this is not a necessary condition. So, in these types of questions, students are advised to use distance formula only.