Question

If (-2,2) and (k,0) are the two diametrically opposite points of a circle of radius 1, then the equation of the circle is:
$
  A. {\text{ }}{{\text{x}}^2} + {y^2} - 2x - 4y - 4 = 0 \\
  B. {\text{ }}{{\text{x}}^2} + {y^2} + 4x - 2y - 4 = 0 \\
  C. {\text{ }}{{\text{x}}^2} + {y^2} - 4x + 2y + 4 = 0 \\
  D. {\text{ }}{{\text{x}}^2} + {y^2} + 4x - 2y + 4 = 0 \\
  E. {\text{ }}{{\text{x}}^2} + {y^2} - 4x - 2y - 4 = 0 \\
 $

Answer 1

Hint – Here we will proceed by finding midpoint M of PQ ends by using the midpoint formula i.e. $\dfrac{{{x_1} + {y_1}}}{2},\dfrac{{{x_2} + {y_2}}}{2}$. Then we will equate given radius with MP i.e. half part of the diameter by using distance formula i.e. $D = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $ to get the required equation.
Complete Step-by-Step solution:

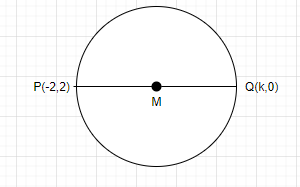
 Since P (-2,2) and Q (k,0) are the endpoints of a diameter. (given)
Therefore, midpoint M of PQ by using the midpoint formula- $\dfrac{{{x_1} + {y_1}}}{2},\dfrac{{{x_2} + {y_2}}}{2}$
Substituting the values of P and Q, we get $ = \dfrac{{ - 2 + k}}{2},\dfrac{{2 + 0}}{2}$
Which means M $ = \left( {\dfrac{K}{2} - 1,1} \right)$
As midpoint divides diameter into two equal parts i.e. radius.
So MP will also be the radius of the circle.
Now we will use distance formula to calculate the equation of radius
 i.e. MP = radius
Formula- $D = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
Where M $ = \left( {\dfrac{K}{2} - 1,1} \right)$
And P (-2,2)
Thus applying formula, we get
 Or $MP = \sqrt {{{\left( { - 2 - \dfrac{k}{2} + 1} \right)}^2} + {{\left( {2 - 1} \right)}^2}} = 1$
Or $\sqrt {{{\left( { - 1 - \dfrac{k}{2}} \right)}^2} + 1} = 1$
$ \Rightarrow 1 + \dfrac{{{k^2}}}{4} + k + 1 = 1$
$ \Rightarrow {k^2} + 4k + 4 = 0$
$ \Rightarrow {\left( {k + 2} \right)^2} = 0$
$ \Rightarrow k = - 2$
Therefore, mid-point M $ = \left( { - \dfrac{2}{2} - 1,1} \right) = \left( { - 2,1} \right)$ which is equal to the centre of the circle.
Hence, equation of circle is-
${\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = {1^2}$
$ \Rightarrow {x^2} + 4x + 4 + {y^2} - 2y + 1 = 1$
Or ${x^2} + {y^2} + 4x - 2y + 4 = 0$
Hence option D is right.
Note – In order to solve this type of question, one can make mistakes to omit the step of calculating the midpoint of the circle which will help in equating the radius with the calculated mid-point. Also we must know the standard form of the circle i.e. ${x^2} + {y^2} + Dx + Ey + F = 0$ where D, E, F are constants to solve similar types of questions.