Question

Ideal fluid flows along a flat tube of constant cross-section, located in a horizontal plane and bent as shown in the figure above (top view). The flow is steady. Are the velocities of the fluid equal at points 1 and 2?

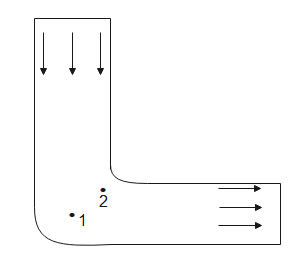
A. Velocity at point 1 is less than the velocity at point 2.
B. Velocity at point 1 is more than the velocity at point 2.
C. Velocity at point 1 is equal to the velocity at point 2.
D. Can't be determined.

Answer 1

Hint: Bernoulli’s equation is the base for fluid mechanics and it is used to manufacture several machines. Machines like pump and diffuser are vastly used in the mechanical industry in order to extract the desired characteristics from the fluid flowing through them. By using Bernoulli’s theorem we can solve this
Formula used:
${P_1} + 0.5\rho {v_1}^2 = {P_2} + 0.5\rho {v_2}^2$

Complete step-by-step solution
It is clearly mentioned that the pipe is in a horizontal plane which means there is no effect of height variation in pressure change. As the fluid is flowing through the pipe its density doesn’t vary.
When an object is rotating in a circle its direction of velocity keeps on changing. When velocity changes there will be an acceleration and this contributes to the force. Now the force which is responsible for the change in direction in case of circular motion is called a centripetal force.
If we see the diagram below

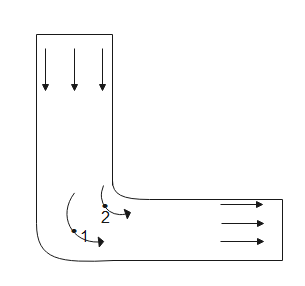
The fluid elements between 1 and 2 are under circular motion. The centrifugal force experienced by the fluid elements is outwards i.e from 2 to 1. That means the pressure at 2 must be greater than the pressure at 1.
${P_2} > {P_1}$
We have Bernouli’s equation
${P_1} + 0.5\rho {v_1}^2 = {P_2} + 0.5\rho {v_2}^2$
From the above equation, since the pressure at 2 is greater than the pressure at 1, the velocity at 2 must be less than the velocity at 1 because velocity should decrease if pressure increases.
${v_1} > {v_2}$
Hence option B is correct.

Note: If we talk about Bernoulli’s law when the wind flows the paper on the calendar will fly up because the pressure under the page will be more and the pressure on the top will be less as the velocity of air on the top of the page is more and the velocity of air at the bottom of the page is less.