Question

How do you solve $x-\ln x=0$?

Answer 1

Hint: We recall the domain and range of the identity function ${{f}_{1}}\left( x \right)=x$ and the logarithmic function${{f}_{2}}\left( x \right)= \ln x$. We recall the solutions of the given function $f\left( x \right)=x-\ln x$ will be at the point of intersection of the curves ${{f}_{1}}\left( x \right)=x$ and ${{f}_{2}}\left( x \right)=\ln x$. We plot the curve and see if there are any points of intersection. \[\]

Complete step-by-step solution:
We are given the following equation to solve
\[x-\ln x=0......\left( 1 \right)\]
We can write the above equation as
\[x=\ln x\]
We are given two functions one is identity function which we denote as ${{f}_{1}}\left( x \right)=x$ and the logarithmic function ${{f}_{2}}\left( x \right)=\ln x$. We know that the graph of ${{f}_{1}}\left( x \right)=x$ is a line passing through origin whose slope is 1 which means inclined at an angle ${{45}^{\circ }}$. We know that graph of logarithm function ${{f}_{2}}\left( x \right)=\ln x$ is the symmetrical curve of the natural exponential function ${{e}^{x}}$.
We also know that the identity function ${{f}_{1}}\left( x \right)=x$ takes real numbers and the same real numbers but logarithmic function ${{f}_{2}}\left( x \right)=\ln x$ takes positive real values and returns real number values. We see that for all $x>0$ we have ${{f}_{1}}\left( x \right)>{{f}_{2}}\left( x \right)$. We can verify it by putting values $\dfrac{1}{e},1,e,{{e}^{2}},...$ in ${{f}_{1}}\left( x \right)$ and ${{f}_{2}}\left( x \right)$.
\[\begin{align}
  & {{f}_{1}}\left( \dfrac{1}{e} \right)=\dfrac{1}{e},{{f}_{2}}\left( \dfrac{1}{e} \right)=-1 \\
 & {{f}_{1}}\left( 1 \right)=1,{{f}_{2}}\left( 1 \right)=0=\ln 1=0 \\
 & {{f}_{1}}\left( e \right)=e,{{f}_{2}}\left( e \right)=\ln e=1 \\
 & {{f}_{1}}\left( {{e}^{2}} \right)={{e}^{2}},{{f}_{3}}\left( {{e}^{2}} \right)=\ln {{e}^{2}}=2 \\
\end{align}\]
We can see that for all $x>0$ we have ${{f}_{1}}\left( x \right)>{{f}_{2}}\left( x \right)$. So ${{f}_{1}}\left( x \right)=x,{{f}_{2}}\left( x \right)=\ln x$ will never intersect each other. We know that the given equation $x-\ln x$ will have solution at point of intersection of the curves ${{f}_{1}}\left( x \right)=x$ and ${{f}_{2}}\left( x \right)=\ln x$. So there will not be any solution for $x-\ln x=0$. We draw the graph below. \[\]

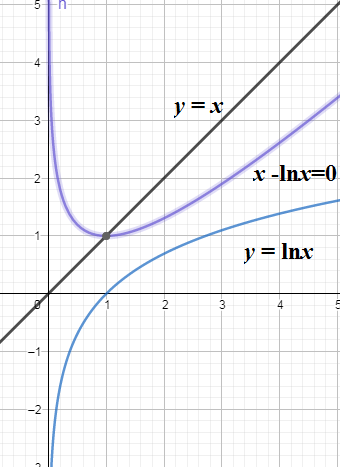
Note: We can alternatively raise both sides of the given equation $x-\ln x=0$ with the base of natural logarithm to have ${{e}^{x-\ln x}}={{e}^{0}}=1$ fro which we get ${{e}^{x}}=x$. We can solve that also by plotting the curve and we shall not get any solution because that ${{e}^{x}}>x$ for all real $x$.